ВОЛЬТ-АМПЕРНЫЕ ХАРАКТЕРИСТИКИ ЭЛЕКТРИЧЕСКИХ ДУГ.
Введение
В работе [1,2] и на странице сайта "Каналовая модель" для гипотетического однородного плазменного канала дуги бесконечной длины получена зависимость, связывающая ток дуги I, радиус канала R и давление в канале p с температурой канала T. Зависимость получена на основе анализа энергобаланса канала в предположении, что неизлучательные потери энергии из канала обусловлены только плазменными поляризационными потерями. Это означает, что на удаление за счет диффузии любой частицы за пределы канала от источника питания дуги затрачивается энергия равная величине снижения энергии частицы в плазме. Энергии снижения различных частиц в плазме (атомов, электронов, ионов) отличаются друг от друга только постоянными множителями порядка единицы, поэтому все они могут быть выражены через величину снижения энергии ионизации атомов χo в плазме канала.
На этой странице на примере дуг, горящих в среде аргона, рассмотрены результаты двух попыток автора сайта на конкретных примерах применить полученную зависимость для расчета вольт-амперных характеристик как каналовых, так и свободно горящих дуг.
Более компактно, чем на упомянутой странице сайта, полученную зависимость можно записать в виде
Эта зависимость записана для системы единиц МКСА. Это означает, что размерность величин, входящих в неё, следующая: ток - в [A], радиус - в [м], давление в - [Па]. Символы в зависимости означают: Ei - потенциал ионизации газа, в котором горит дуга, k - постоянная Больцмана, величина δ= W/Õ учитывает долю излучательных потерь энергии W из канала дуги относительно поляризационных потерь энергии Õ из канала, Z1 и Zo - статистические суммы ионов и атомов плазмообразующего газа, μ - относительный атомный вес плазмообразующего газа, Qeo и Qe1 - эффективные сечения столкновения электронов с атомами и ионами плазмообразующего газа, η - степень ионизации плазмы, τ=χo/kT - параметр, характеризующий величину снижения энергии ионизации атомов в плазме относительно поступательной энергии частиц плазмы, ψ - отношение скорости электронов в плазме к скорости тяжелых частиц (атомов, ионов).
Посмотрим, как зависят значения H от температуры для случая дуги в
аргоне, используя опубликованные в литературе данные.
Для расчетов
понадобятся данные о термодинамическом составе плазмы аргона, которые возмем из работы [3].
Для оценки сечений воспользуемся теоретическими расчетами, приведенными в [3], но так как расчеты
сечений у разных авторов сильно различаются,
 то для определенности используем графики,
помеченные ссылкой [54,55], которые занимают промежуточное положение среди
рассматриваемых зависимостей.
то для определенности используем графики,
помеченные ссылкой [54,55], которые занимают промежуточное положение среди
рассматриваемых зависимостей.
Энергию ионизации аргона примем равной
Ei= 15,8 эв. Значения статистических сумм равны Zo=1 и
Z1=6. Относительный атомный вес аргона η=40. Величина
ψ=267.
Полагаем также,
что для дуг атмосферного давления потерями на излучение можно пренебречь, то есть считать, что
δ=0.
Необходимые для оценок данные, перечисленные выше, запишем в 1-3 и 6-7 столбцах следующей таблицы.
Степень ионизации плазмы η= ne/no раcсчитаем, исходя
из термодинамического состава.
Относительную величину снижения энергии ионизации τ=χo/kT рассчитаем также
из термодинамического состава, найдя предварительно величину снижения энергии ионизации атомов
χo=2,9·10-8(ne/kT)1/2 (здесь χo -
в эв, ne - в см-3, T - в K).
С учетом сказанного рабочую формулу для обсчета выражения (2) для аргоновых дуг запишем в следующем виде
Проведенный оценочный расчет с использованными значениями сечений показывает (таблица), что модельные значения H лежат в пределах от 0,8·10 -4 до 1,3·10 -4 для области температур плазмы от 7000K до 11000K, то есть в диапазоне существования каналовых дуг.
|
|
no, м-3 | ne, м-3 | τ | η | Qeo, м2 | Qe1, м2 | |
| 1,22·1024 | 2,94·1019 | 0,39·10-2 | 2,40·10-5 | 3,5·10-20 | 9,1·10-17 | 1,65·10-4 | |
| 1,05· 1024 | 2,72· 1020 | 0,94· 10-2 | 2,59· 10-4 | 4,0· 10-20 | 6,2·10-17 | 0,89·10-4 | |
|
|
9,15· 1023 | 1,45· 1021 | 1,56· 10-2 | 1,58· 10-3 | 4,2·10-20 | 3,8·10-17 | 1,29·10-4 |
|
|
8,95· 1023 | 5,34· 1021 | 2,66· 10-2 | 5,97· 10-3 | 5,5·10-20 | 2,8·10-17 | 1,20·10-4 |
|
|
7,04· 1023 | 1,51· 1022 | 4,00· 10-2 | 2,14· 10-2 | 6,0·10-20 | 2,0·10-17 | 0,96·10-4 |
|
|
5,97· 1023 | 3,46· 1022 | 5,17· 10-2 | 5,80· 10-2 | 6,2·10-20 | 1,6·10-17 | 0,80·10-4 |
|
|
4,80· 1023 | 6,66· 1022 | 6,50· 10-2 | 13,9· 10-2 | 6,7·10-20 | 1,3·10-17 | 0,67·10-4 |
Сопоставление выражения (1) с эмпирическими зависимостями показало ("Каналовая модель"), что для описания каналовых дуг подходит постоянное значение H=1,622·10-4 (или lgH = -3,79) , которое согласуется с полученными оценками [1,2]. Поэтому этим "откалиброванным" значением H будем пользоваться в расчетах, проводимых на этой странице.
Вольт-амперные характеристики каналовых дуг
Постоянство величины H означает, что левая часть выражения (1) зависит только от температуры, а правая - только от тока, радиуса канала и давления. Но, при этом эти части остаются равными друг другу, а это свидетельствует о том, что каждому значению температуры соответствует бесчисленное множество комбинаций из величин тока, радиуса и давления.
Правая часть зависит от трех независимых величин - тока, радиуса и давления, характеризующих плазменный канал. Но если ток и давление мы можем задать по своему произволу, то радиус плазменного канала задать заранее не всегда возможно. Это удается сделать только в каналовых дугах, то есть дугах, канал которых обычно стабилизирован водоохлаждаемыми медными шайбами. При достаточно большом токе в каналовой дуге радиус плазменного канала не сильно отличаеться от радиуса канала в водоохлаждаемых шайбах. Вот такие режимы и можно описывать зависимостью (1).
Обозначим левую часть формулы (1), которая явно зависит только от температуры, через B(T) и запишем выражение
С помощью этих двух формул можно определить величину температуры в дуге, для которой известны величина тока I и радиус канала R. Действительно, с помощью (5) находим сначала соответствующее значение B(I,R), а так как B(I,R) численно совпадает c B(T), то из выражения (4) определяется величина температуры канала T.
Зависимость B(T) была подробно рассчитана в 1979 г., результаты этого расчета были представлены в виде графика T=T(lgB(T)) в работе [1,2], а впоследствии и на странице этого сайта ("Каналовая модель"). По опубликованному графику можно определить температуру каналовой дуги при конкретных значениях тока I и радиуса канала R. Для этого нужно рассчитать величину логарифма lgB(I,R) выражения (5), что не представляет особых затруднений, и, учитывая, что B(I,R)=B(T), по графику T=T(lgB(T)) определить величину температуры T в дуге.
Если известна зависимость удельной электропроводности плазмы канала дуги от температуры σ=σ(T), то это позволяет определить величину напряженности электрического поля в канале дуги E=E(I,R), то есть вольт-амперную характеристику плазменного канала. Рассчитывается она по формуле
Здесь G - электропроводность однородного плазменного канала.
Численно обрабатывать зависимости (4-6) с помощью инженерного калькулятора утомительно. Ускорить обработку позволяет персональный компютер с установленной программой Microsoft Small Basic. Small Basic представляет язык программирования начального уровня, простой и доступный. Последняя версия его появилась в 2011 г.
Ниже приведены листинги программ, написанных на упомянутом языке автором сайта, для обработки зависимостей (4-6).
Программа ProgB(T) предназначена для вывода на экран значений выражения B(T) (4) в зависимости от температуры. Скриншот листинга этой программы с экрана монитора представлен на рис.01. Начальный участок оцифровки B(T), выполненный программой при ее вызове, показан в качестве примера на рис.02.
Программа ProgSigma при вызове выводит на экран значения удельной электропроводности плазмы при различных значениях температуры. Так как используемая теоретическая зависимость для удельной электропроводности плазмы известна в виде графика, то её график был предварительно преобразован к виду, удобному для оцифровки. Для этого на графике зависимости был выбран ряд точек и соседние точки были соединены отрезками прямых линий. Выбор точек сделан с таким расчетом, чтобы ординаты реальной зависимости минимально отличались от ординат проведенных отрезков. Таким образом, реальная зависимость заменяется ломаной линией из прямолинейных отрезков, которая легко оцифровывается. Скриншот программы ProgSigma для оцифровки зависимости приведен на рис.03, 04 и 05, а результат оцифровки начального участка этой зависимости изображен на рис.06.
Для удобства работы написана программа ProgB(I,R) для вычисления величины B(I,R) (5). Но написана она не для вычисления конкретного значения B(I,R), а для вычисления целого ряда значений B(I,R) при различных значениях R, но неизменном значении тока. При вызове эта программа запрашивает сначала величину шага дискретизации радиуса и после введения его предлагает ввести с клавиатуры величину тока дуги c подтверждением, после чего выводит на экран целый ряд значений значение B(I,R) с заданным шагом дискретизации R. Скриншот программы ProgB(I,R) представлен на рис.07, а изображение, выводимое ею на экран, показано на рис.08.
Программа ProgE написана для обсчета зависимости (6). Скриншот листинга программы ProgE представлен на рис.09 и 10. После вызова эта программа предлагает сначала ввести с клавиатуры величину тока с подтверждением, потом величину радиуса дуги с подтверждением и, наконец, значение удельной электропроводности плазмы. После подтверждения последнего ввода программа выводит на экран значения электропроводности канала дуги G и напряженности электрического поля E в канале. На экране монитора это выглядит, как рис.011.
Для определения напряженности электрического поля в дуге с помощью перечисленных программ нужно открыть в Small Basic на экранe монитора программы ProgB(I,R), ProgB(T), ProgSigma и ProgE, а затем выполнить последовательно следующие четыре однотипные действия: 1.Запустить программу ProgB(I,R) и по заданным значениям тока I и радиуса R определить значение B(I,R). 2. Запустить программу ProgB(T) и по полученному значению B(I,R)определить температуру плазмы. 3. Запустить программу ProgSigma и по полученному значению температуры определить величину электропроводности плазмы. 4.Запустить программу ProgE и ввести в неё последовательно величины тока, радиуса и электропроводности и в итоге считать с экрана монитора величину напряженности поля в дуге.
Проиллюстрирую сказанное на примере следующей экспериментальной работы [4] по исследованию аргоновых дуг
при атмосферном давлении. В каналовых электрических
дугах с диаметром стабилизирующего канала в медных шайбах 4, 6 и 8 мм была измерена наряженность электрического
поля в зависимости от тока.
Эти результаты представлены следующими графиками 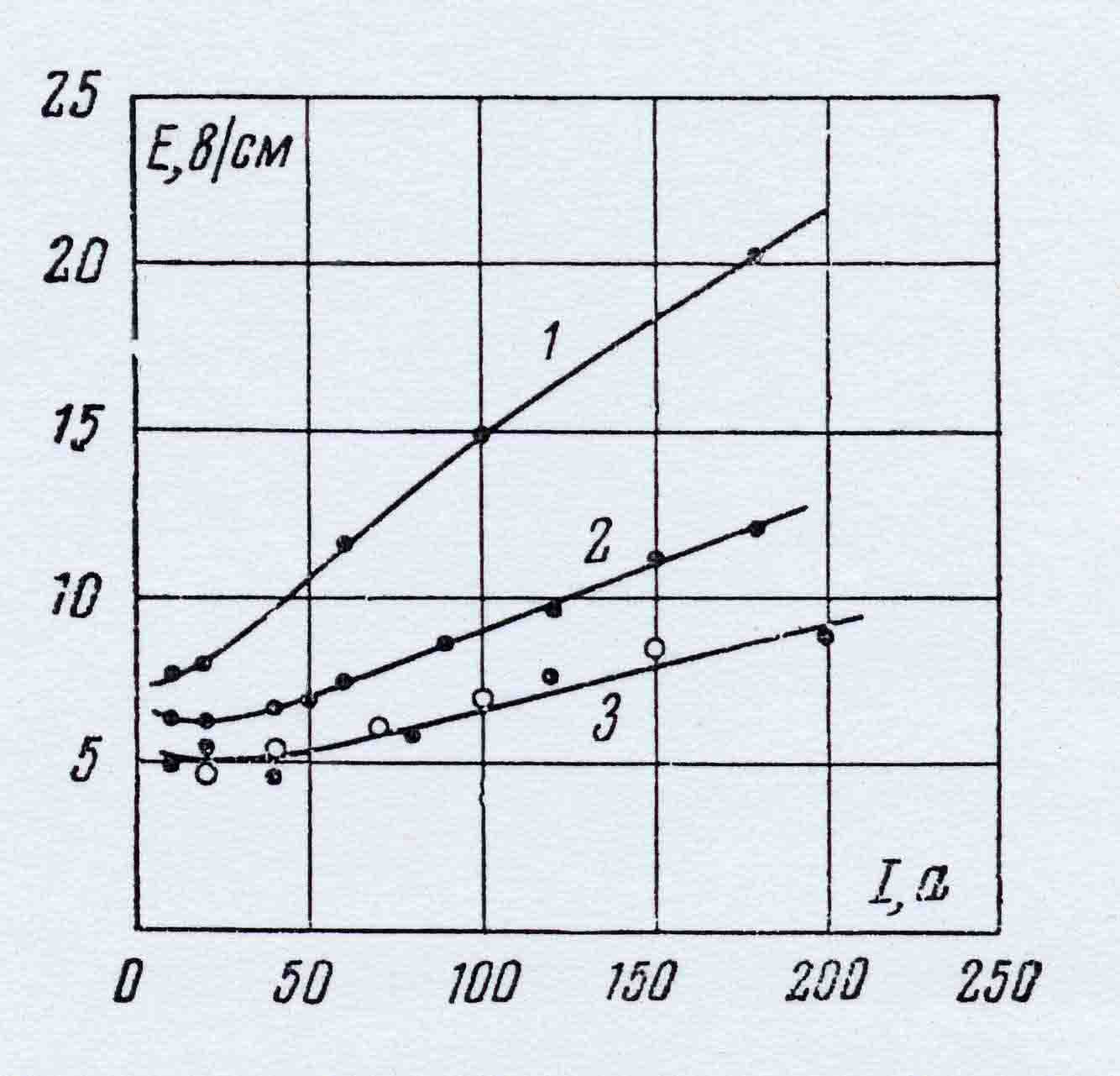 с нанесенными на них экспериментальными точками. Графики 1, 2 и 3 относятся, соответственно, к дугам с диаметром
канала 4, 6 и 8 мм.
с нанесенными на них экспериментальными точками. Графики 1, 2 и 3 относятся, соответственно, к дугам с диаметром
канала 4, 6 и 8 мм.
На данной странице результаты в экспериментальных точках представлены в первых двух строчках нижеследующих таблиц.
А в третьей строчке таблиц приведена рассчитанная на основе этих результатов
средняя по сечению дуг удельная электропроводность плазмы аргона.
| Каналовая дуга с диаметром канала 4 мм (R=2·10-3, м) | |||||
| 10 | 19 | 60 | 100 | 180 | |
| 7,74 | 8,15 | 11,66 | 14,94 | 20,23 | |
| 10,28 | 18,55 | 40,95 | 53,26 | 70,80 | |
| 1,02 | 1,94 | 6,12 | 10,02 | 18,35 | |
| 8180 | 9100 | 11400 | 12780 | 14820 | |
| 9,45 | 17,9 | 44,2 | 60,6 | 86 | |
|
|
8,42 | 8,45 | 10,80 | 13,13 | 16,66 |
| Каналовая дуга с диаметром канала 6 мм (R=3·10-3, м) | |||||||||
| 10 | 19 | 40,7 | 49,5 | 60 | 89,5 | 122 | 151 | 180 | |
| 6,54 | 5,95 | 6,72 | 7,14 | 7,50 | 8,70 | 9,76 | 11,31 | 12,2 | |
| 5,41 | 11,29 | 21,42 | 24,52 | 28,30 | 36,38 | 44,21 | 47,22 | 52,18 | |
| 0,55 | 1,05 | 2,26 | 2,48 | 3,33 | 4,97 | 6,77 | 8,38 | 9,99 | |
| 7440 | 8200 | 9360 | 9520 | 10060 | 10680 | 11640 | 12220 | 12700 | |
| 5,80 | 9,55 | 21,63 | 23,30 | 28,98 | 36,02 | 46,91 | 53,80 | 60,07 | |
|
|
6,10 | 7,04 | 6,55 | 7,51 | 7,32 | 8,79 | 9,20 | 9,93 | 10,06 |
| Каналовая дуга с диаметром канала 8 мм (R=4·10-3, м) | |||||
| 20,3 | 40,7 | 69,8 | 100,6 | 150 | |
| 4,76 | 5,33 | 6,25 | 7,14 | 8,48 | |
| 8,48 | 14,64 | 22,22 | 28,03 | 35,20 | |
| 0,73 | 1,47 | 2,51 | 3,63 | 5,41 | |
| 7760 | 8660 | 9540 | 10080 | 11080 | |
| 7,38 | 14,34 | 23,51 | 29,21 | 40,56 | |
|
|
5,47 | 5,65 | 5,91 | 7,26 | 7,36 |
| Каналовая дуга с диаметром канала 8 мм (R=4·10-3, м) | ||||||
| 10 | 19 | 39 | 79,9 | 120 | 200 | |
| 5,12 | 5,60 | 4,76 | 5,95 | 7,74 | 8,92 | |
| 3,88 | 6,75 | 16,30 | 26,64 | 30,84 | 44,60 | |
| 0,36 | 0,68 | 1,40 | 2,88 | 4,33 | 7,21 | |
| 7000 | 7680 | 8600 | 9780 | 10590 | 12150 | |
| 3,63 | 6,98 | 13,72 | 26,01 | 34,70 | 52,90 | |
|
|
5,48 | 5,41 | 5,66 | 6,11 | 6,88 | 7,52 |
Рассчитаем значения электропроводности плазмы и напряженности поля для указанных режимов дуг с помощью приведенных программ. В качестве исходных данных для расчета считаем известными радиус канала дуги и величину тока дуги. Обработку исходных данных проводим следующим образом. С помощью программы ProgB(I,R) находим для каждого режима значения B(I,R) (4-я строка таблиц). Затем с помощью программы ProgB(T) определяем температуру канала дуги T (5-я строка таблиц). Потом с помощью программы ProgSigma нужно определить величину удельной электропроводности плазмы (6-я строка таблиц) и в итоге с помощью программы ProgE рассчитать величину напряженности электрического поля в дуге (7-я строчка таблиц). Однако, при выполнении последних двух шагов возникло следующее затруднение.
Точность иллюстрируемого расчета, кроме всего прочего,
зависит от того,
насколько хорошо используемая при расчете зависимость σ(T) соответствует действительности. По состоянию на 1987г. наши
сведения по этому
вопросу отражают следующие графики, полученные еще до 1972 г.[3]. Поэтому выбор наиболее подходящей зависимости был произведен методом проб. И этот метод показал (хотя мог и не показать), что наиболее
удовлетворительно расчетные значения электрического поля в дугах согласуются с экспериментальными в случае использования теоретической зависимости
[5], которая помечена ссылкой под номером 59 и отображена прерывистой линией из тире-точка-тире-точка. Поэтому этот
график был оцифрован и листинг программы ProgSigma для представления этого графика в табличном виде приведен на этой странице.
Поэтому выбор наиболее подходящей зависимости был произведен методом проб. И этот метод показал (хотя мог и не показать), что наиболее
удовлетворительно расчетные значения электрического поля в дугах согласуются с экспериментальными в случае использования теоретической зависимости
[5], которая помечена ссылкой под номером 59 и отображена прерывистой линией из тире-точка-тире-точка. Поэтому этот
график был оцифрован и листинг программы ProgSigma для представления этого графика в табличном виде приведен на этой странице.
Сравнение 2-ой и 7-ой строчек таблиц показывает удовлетворительное согласие расчетных и экспериментальных значений напряженности электрического поля
в случае использования упомянутой зависимости для электропроводности плазмы аргона.
Вольт-амперная характеристика свободно горящей дуги при атмосферном давлении.
Если с помощью зависимости (1) проанализировать ограниченные твердыми стенками дуги, которые горят при одном и том же значении тока, но имеют каналы различного радиуса, то обнаружим, что электропроводность канала дуг G с возрастанием радиуса канала сначала увеличивается, а затем при дальнейшем увеличении радиуса начинает убывать, то есть электропроводность имеет максимум при каком то значении радиуса. Это означает, что дуга с максимальной электропроводностью G обладает минимальной напряженностью электрического поля E, а, следовательно, потребляет и минимальную мощность от источника тока.
Если посмотреть на свободно горящую дугу в атмосфере какого-либо газа, то можно сказать, что канал свободно горящей дуги также ограничен стенками, но только не жесткими, а "эластичными" газообразными. В этих условиях естественно ожидать, что радиус свободно горящей дуги принимает такое значение, при котором мощность, потребляемая дугой, минимальна. Вспомним по этому поводу известный принцип минимума мощности Штеенбека [6].
Проиллюстрируем на примере 60-ти амперной свободно горящей при атмосферном давлении аргоновой дуги расчет напряженности электрического поля в плазменном канале дуги. Ход расчета представим в следующей таблице.
| Расчет напряженности электрического поля в канале свободной дуги в аргоне при атмосферном давлении. Ток дуги 60 А. | |||||||
| 14 | 17 | 21 | 23 | 24 | 25 | 30 | |
| 0,33 | 0,247 | 0,18 | 0,157 | 0,147 | 0,138 | 0,105 | |
| 6920 | 6640 | 6380 | 6280 | 6220 | 6160 | 5960 | |
| 3,40 | 2,60 | 1,86 | 1,58 | 1,41 | 1,24 | 0,73 | |
| 2,87 | 2,54 | 2,33 | 2,29 | 2,36 | 2,47 | 2,75 | |
Здесь с помощью программы ProgB(I,R) рассчитаны значения B(60,R) для дуг различного радиуса. Затем с помощью программы ProgB(T) определены модельные температуры в дугах. На следующем этапе с помощью программы ProgSigma определены удельные электропроводности плазмы дуг. И на последнем этапе с помощью ProgE(I,R) рассчитаны напряженности электрического поля в дугах различного радиуса. В соответствии со сказанным выше из этих расчетов следует, что свободно горящая 60-ти амперная дуга имеет радиус канала равный 23 мм, а напряженность электрического поля в канале равняется величине 2,29 В/см.
Рассчитаем теперь вольт-амперную характеристику свободной дуги в аргоне и сопоставим ее с
известной экспериментальной зависимостью из [6],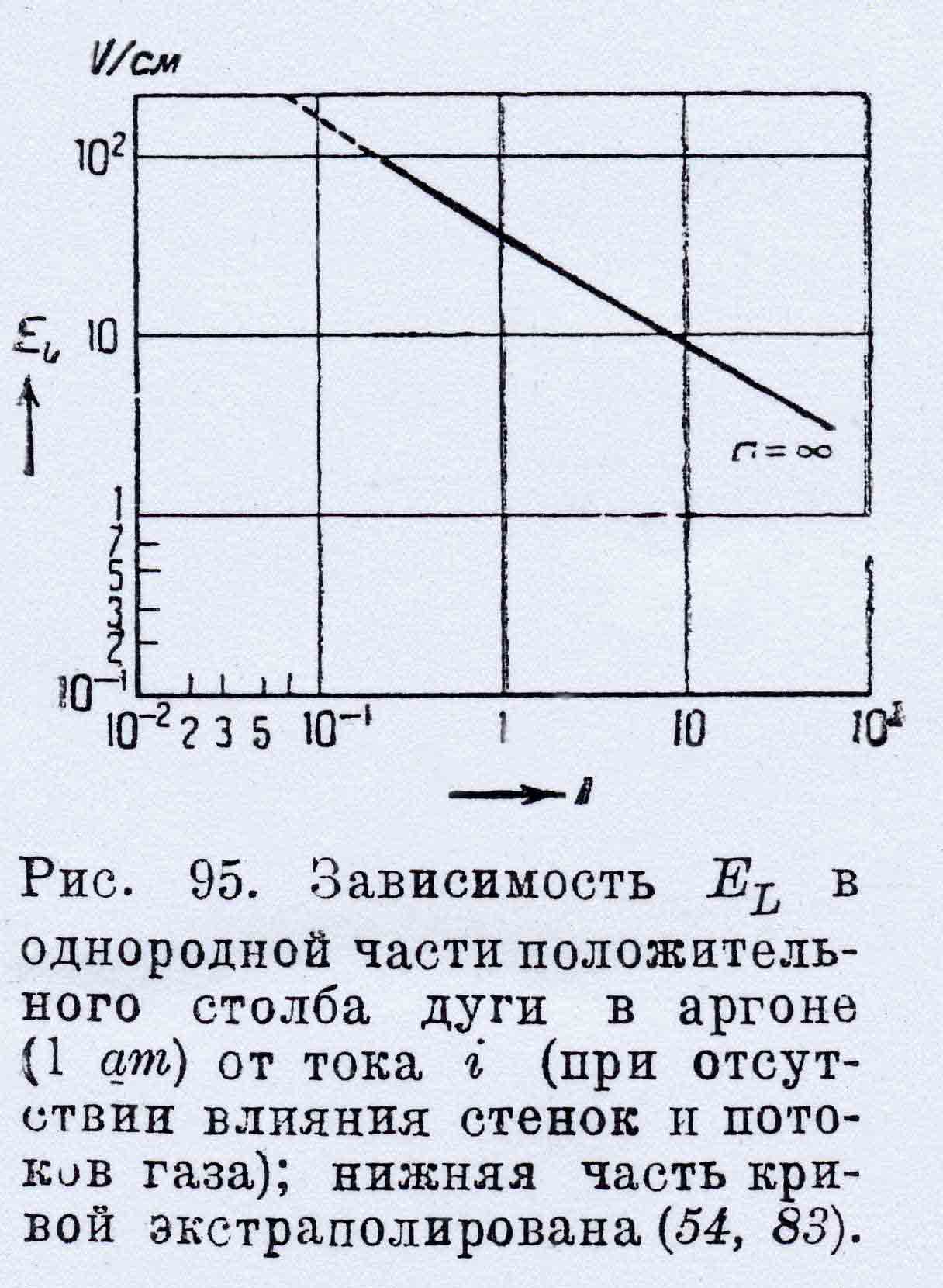 изображенной на графике слева. Как видно из графика, зависимость lgE от lgI очень близка к линейной.
изображенной на графике слева. Как видно из графика, зависимость lgE от lgI очень близка к линейной.
В следующей
таблице приведены результаты сравнения значений напряженностей электрического поля из этой зависимости
и значений, рассчитанных по формуле (1) для нескольких величин тока.
| Сопоставление экспериментальных данных из [6] с результатами расчета по (1). | |||||||
| 10 | 30 | 60 | 100 | 200 | 1000 | 10000 | |
| 8,97 | 4,66 | 3,08 | |||||
| 4,18 | 2,94 | 2,29 | 1,96 | 1,57 | 0,92 | 0,43 | |
| 6,4 | 13 | 23 | 31 | 44 | 140 | 650 | |
| 6380 | 6400 | 6280 | 6320 | 6460 | 6350 | 6350 | |
Как видно из таблицы, налицо тенденция сближения экспериментальных и расчетных значений, это можно объяснить тем, что с ростом тока растет и радиус канала дуги R, а канал большего радиуса меньше отклоняется по параметрам от однородного канала, чем канал малого радиуса. Это позволяет предположить, что при достаточно больших токах экспериментальные и расчетные значения будут практически совпадать.
Анализ расчетных значений величин, касающихся свободных дуг, которые приведены в
последней таблице, приводит к ряду важных выводов. Но прежде, чем делать их, напомню, что
учет плазменных поляризационных процессов приводит к выражению, лежащему в основе зависимости (1), которое в упрощенной форме
можно сформулировать следующим образом. Неизлучательные (поляризационные) потери энергии из
токопроводящего канала дуги равны произведению величины χo снижения энергии ионизации атомов в канале на
число частиц (атомов, электронов, ионов), удаляемых через границу канала в единицу времени за счет процессов диффузии. После этого напоминания сформулируем выводы:
1. Рассчитанные значения температуры (таблица) показывают, что температура свободных дуг практически не зависит от тока.
В свою очередь, если постоянна температура, то постоянны величина χo
и скорости диффузионных процессов на границе канала. А это означает, что с изменением
тока неизлучательные (поляризационные) потери из канала регулируются в основном
за счет изменения радиуса канала дуги, так как только в этом случае меняется общее число частиц, удаляемых из канала, а, следовательно, и мощность неизлучательных потерь.
2. В каналовых дугах радиус канала постоянен, поэтому потери
энергии из канала регулируются за счет изменения величины снижения энергии ионизации χo и скорости диффузионных процессов через границу канала.
А так как повлиять на эти величины можно только за счет температуры, то в каналовых дугах температура
существенно зависит от тока.
3. Дугу, стабилизированную цилиндрической трубкой, при токе I и давлении p можно считать каналовой, если радиус
стабилизирующей трубки меньше радиуса канала свободно горящей дуги при тех же значениях тока и давления.
Заключение.
В заключение хочу отметить, что цель написания этой страницы направлена не столько на рассмотрение ВАХ дуг, при желании о них можно рассказать существенно больше, сколько на то, чтобы лишний раз подчеркнуть фундаментальную роль поляризационных плазменных процессов в электрических разрядах.
Л И Т Е Р А Т У Р А
- Пышнов А.В. К вопросу построения модели канала квазистационарной
сильноточной
ограниченной стенками дуги. - М.: Деп. ВИНИТИ № 6889-В89 1989. 35 с. - Пышнов А.В. //ТВТ. 1990. Т. 28. № 2. С. 410.
- Физика и техника низкотемпературной плазмы. Под ред. Дресвина С.В. - М.: Атомиздат, 1972. 352 с.
- Асиновский Э.И., Кириллин А.В. //ТВТ. 1965. Т.3. № 4. С. 677.
- De-Voto R.S. //Phys. Fluids. 1967. V. 10. № 2.
- А.Энгель и М.Штенбек. Физика и техника электрического разряда в газах, т.II:
Пер. с нем./Под ред. Капцова Н.А. -М.; Л.: ОНТИ, 1936.
Страница написана в январе 2012 г., Москва.
В конце июня на странице сделаны поправки (см. "Хронология сайта").