ЭНЕРГОБАЛАНС АРГОНОВОЙ ДУГИ С УЧЕТОМ ПОЛЯРИЗАЦИИ
Целью настоящей страницы является иллюстрация того, что поляризационные потери Qпп из канала сильноточного разряда существенно превышают остальные виды неизлучательных потерь, как об этом заявлено на странице "Роль поляризации плазмы". Напрямую убедиться в этом позволяет анализ радиальных распределений температуры, приведенных в научных статьях, диссертациях. Попытка опубликовать в виде краткого сообщения один из таких анализов, предпринятая около десяти лет тому назад, закончилась отказом. Представляется, что рецензент не воспринял смысла работы. Ниже приводится текст этого сообщения, доработанный на основе замечаний первой рецензии, приведенной в конце сообщения, кроме того, при подготовке этой страницы сайта написано дополнение, более полно иллюстрирующее основную мысль этого сообщения.
Краткое сообщение, посланное в 1996 г. в журнал для опубликования, называлось:
АНАЛИЗ ПОТЕРЬ ЭНЕРГИИ ИЗ КАНАЛА ЭЛЕКТРИЧЕСКОЙ ДУГИ С УЧЕТОМ ПОЛЯРИЗАЦИОННЫХ ПРОЦЕССОВ
Анализ экспериментальных данных указывает, что неизлучательные потери энергии из канала электрической дуги тесно связаны с поляризационными процессами в плазме канала. Это обусловлено тем, энергия частиц в плазме меньше, чем энергия тех же частиц, но находящихся в нейтральной среде [1]. В настоящей работе иллюстрируется, что величина неизлучательных потерь энергии из канала дуги определяется в основном поляризационными процессами.
Роль поляризации плазмы рассмотрим в наиболее простом случае, когда в канале дуги первую роль играет процесс снижения энергии ионизации атомов. Рассмотрим однородный по длине и цилиндрически симметричный канал электрической дуги в аргоне. Вследствие однородности и симметрии все физические величины являются функциями только текущего радиуса канала r. Плазма такого канала состоит из атомов с концентрацией no(r), их положительных ионов с концентрацией n1(r) и электронов с концентрацией ne(r). Процессы поляризации с участием атомов будут преобладать при режимах дуги, для которых выполняется условие no(r)>>ne(r).
Здесь ne - в см-3 , T - температура в K.
Величина χo на несколько порядков меньше величины Ео самой энергии ионизации, поэтому для удобства сопоставления χo со значениями температуры частиц в канале дуги будем пользоваться величиной k-1χо, имеющей размерность температуры, k- постоянная Больцмана.
Рис.1. На рисунке изображена зависимость k-1χо(T) для аргоновой плазмы атмосферного давления, рассчитанная по формуле (1). При построении графика использованы данные о составе плазмы при различных значениях температуры, приведенные в работах [2,3].
На основе экспериментального радиального распределения температуры в канале аргоновой дуги T(r) построено радиальное распределение величины снижения энергии ионизации атомов k-1χо(r) (рис. 2) с помощью графика на рис.1. Построение выполнено для режима дуги, горящей при атмосферном давлении. Ток дуги I=60 А, напряженность электрического поля в канале E=7,3 В/см. Радиальные распределения температуры T(r) для этого тока, а также ряда других значений тока, опубликованы в работе [4].
Рис.2. Радиальные распределения величин снижения энергии ионизации атомов k-1χo(r) (кривая 3) и температуры T(r) в канале аргоновой дуги, стабилизированной кварцевой трубкой 4 с внутренним диаметром 6,4 мм. Кривая 1 - радиальное распределение температуры, полученное авторами работы [4] на основе обработки результатов спектроскопических измерений с использованием заниженных значений вероятностей переходов. Кривая 2 - радиальное распределение температуры, после обработки результатов измерений с использованием исправленных значений вероятностей переходов. Зависимость 3 относится к кривой 2.
Энергия ионизации атомов в плазме равна Eo-χo(r), где Eo - энергия ионизации изолированного атома. Энергия ионизации изолированного атома является внутренней энергией атома. Энергия ионизации атомов в плазме также является внутренней энергией, но уже зависящей от параметров плазмы. Параметры квазистационарной плазмы можно считать зависящими только от координат, поэтому энергия ионизации также зависит только от координат. Такой вид зависимости характерен для потенциальных форм энергии, поэтому условно можно сказать, что атомы в канале дуги находятся в потенциальной яме χo(r).
Электрическая дуга поглощает энергию внешнего источника тока. Поглощение энергии происходит в тех областях дуги, в которых электропроводность плазмы отлична от нуля. Ограниченную радиусом R центральную область дуги, в которой поглощается подавляющая часть энергии внешнего источника, например, не менее 90%, будем называть каналом дуги. За пределами R начинается область горячего, но уже практически непроводящего газа, окружающего канал. При подходе к границе канала температура плазмы начинает быстро убывать, одновременно происходит и резкое уменьшение таких параметров плазмы канала, как электропроводность и снижение величины энергии ионизации, до пренебрежимо малых значений. Это определение радиуса канала не четкое, но другое, по-видимому, придумать сложно (рис. 2).
Потенциальная яма χo(r) вызывает радиальный поток атомов от периферии к оси канала, поскольку атомы стремятся перемещаться в зоны, где энергия ионизации меньше. С другой стороны, для поддержания стационарности канала атомы должны удаляться за его пределы в адекватном количестве.
Для удаления атома, находящегося в точке ρ , за пределы канала ему нужно сообщить порцию энергии ΔEo(ρ), равную
величиной χo(R) можно пренебречь (рис. 2).
С учетом (2) можно сказать, что <ΔEo> равна средней величине снижения энергии ионизации в канале < -χo> в расчете на атом.
Отметим, что атомы, удаляемые за пределы канала, являются достаточно «горячими» и сами служат источниками энергии для нагрева среды, окружающей канал, т.е. канал дуги является источником тепла. Но в данной работе эти внешние по отношению к каналу процессы не рассматриваются, они освещены в литературе.
Здесь vo - скорость атомов, μ - относительный атомный вес, mo - атомная единица массы. Выражения (4) представляют собой классические выражения для потоков, вытекающие из газокинетических представлений. Этими представлениями можно пользоваться, так как на границе R вещество является практически сильно нагретым газом, а не плазмой. Как записать выражения для потоков в самой плазме, ответить трудно, так как в плазме проявляется сильное коллективное взаимодействие частиц, теория которого не разработана.
Мощность qχ черпается из внешнего источника тока, обеспечивающего существование дуги. Потери энергии из канала складываются из потерь на излучение и неизлучательные потери. Потери энергии на излучение в дугах обычно малы. Для режима на рис. 2 их можно оценить величиной около 10-15%. Потерями энергии из канала за счет отвода ее на электроды пренебрегаем в силу допущения однородности канала по длине. Заметим, что канал становится тем более однородным по длине, чем больше длина его превышает радиус канала. Для режима на рис. 2 это условие хорошо выполняется. Поэтому можно сказать, что подавляющая часть энергии внешнего источника тока расходуется на неизлучательные потери энергии.
Здесь E - напряженность электрического поля в столбе дуги, I - ток дуги.
Сравнение численных значений выражений выражений (5) и (6) позволяет оценить роль поляризационных процессов в энергобалансе электической дуги. Сравним эти значения для режимов на рис. 2.
Согласно введенному выше определению радиуса R, его значение для этого случая находится в пределах 3,10 ÷ 3,16 мм. Этому интервалу значений R соответствуют согласно (6) значения qE в интервале 220 ÷ 225 вт/см2 .
Величина qχ , полученная из обработки оригинального распределения Т(r) на рис.2 (кривая 1) с помощью формул (3-5), составляет 316 вт/см2 , то есть она приблизительно на 40% превышает значение qE . Завышенное значение qχ согласно анализу, выполненному в [5], можно объяснить тем, что при обработке результатов спектроскопических измерений температуры в работе [4] использованы заниженные в ~ 2 раза вероятности переходов. Причем возможность завышения температуры по этой причине допускается и самими авторами [4]. Значение qχ, рассчитанное на основе обработки радиального распределения на рис. 2 (кривая 2), которое получено с использованием исправленных значений вероятностей переходов, составляет 212 ÷ 260 вт/см2. Причем меньшему значению R соответствует большее значение qE и меньшее значение qχ.
С учетом сказанного значения величин qE и qχ можно считать совпадающими в пределах погрешностей. На основании этого можно сказать, что неизлучательные потери, действительно, определяются в основном поляризационными потерями.
Следует отметить, что ошибки в определении радиуса канала R заметно сказываются на величине qχ. Из приведенных значений видно, что 2% ошибка в определении радиуса может привести к 20% ошибке в величине qχ. Поэтому на основе полученного результата можно сказать только то, что потеря энергии на увеличение внутренней энергии атомов, удаляемых за пределы канала разряда, является преобладающей. Выяснить вклад в потери энергии других возможных механизмов неизлучательных потерь энергии в этой ситуации не удается.
Как показывает анализ соответствующих распределений T(r) из [4] для других величин (30,40 и 50 А) тока дуги, выражение (5) остается справедливым и для этих значений.
В итоге можно предварительно сказать, что зависимость (5), учитывающая плазменные поляризационные эффекты, правильно описывает неизлучательные потери из канала электрической дуги.
На этом краткое сообщение заканчивалось. Привожу самую первую рецензию на это сообщение, вторая рецензия мало чем от нее отличается, и решение редколлегии по этому сообщению. Кроме того, прилагаю к краткому сообщению дополнение, которое было написано при подготовке этой странички сайта.
Дополнение к краткому сообщению.
На основе проведенного анализа можно сказать, что удельная мощность (в расчете на единицу поверхности канала радиуса R), необходимая для поддержания канала в стационарном состоянии, равна произведению среднего значения величины снижения энергии ионизации атома в канала на величину потока атомов на границе канала. Напомню, что величина потока является скалярной величиной, то есть величиной, не зависящей от направления.
Таким образом, выражение (5), на вид очень простое, оперирует со средней величиной снижения энергии ионизации в канале и величиной потока на границе канала. Априорно значения этих величин неизвестны, а экспериментальное их определение представляет сложную задачу. Видимо, из-за этого зависимость (5) до настоящего времени ускользала от внимания исследователей. Добраться до нее удалось сложным окольным путем, о котором рассказано на предыдущих страницах этого сайта. В связи с этим представляется, что практическая ценность выражения (5) незначительна, но это только на первый взгляд.
Для однородного гипотетического канала дуги эти параметры легко рассчитываются. Поэтому из анализа энергобаланса, проведенного с однородным модельным вариантом выражения (5), вытекает аналитическая модельная зависимость температуры от тока, давления, радиуса канала и рода плазмообразующего газа.
Выражение модельной температуры для однородного гипотетического канала, полученное в работе [7, 9], выглядит следующим образом:
Здесь I - ток дуги, R - радиус канала, p - давление в канале дуги, T - температура однородного модельного канала, Ei - потенциал ионизации плазмообразующего газа. Величина H включает в себя внутренние параметры канала дуги. Один из таких параметров δ=W/Q, учитывающий мощность излучения из канала дуги W, выделим особо:
Сопоставление формулы (7) было проведено с экспериментальными данными, относящимися к аргоновым каналовым дугам, как наиболее полно изученным экспериментально.
Сравнение зависимости (7) с экспериментальными значениями средней температуры в канале аргоновых дуг атмосферного давления при одинаковых внешних параметрах (ток, радиус, род газа) показало, что величину Ho можно считать постоянной и равной Ho=1,495· 10-4, если размерность, входящих в формулу величин следующая: А, м, Па. Это значение Ho получено в предположении, что доля излучательных потерь в анализируемых случаях составляла 15% от подводимой электрической мощности. При этом анализировался диапазон режимов каналовых дуг, соответствующий интервалу средних температур от 7000 до 11500К.
Таким образом, основываясь на данных экспериментов, можно сказать, что выражение (7) позволяет рассчитывать величину средней температуры в канале дуги.
Величина средней температуры в канале дуги приводится редко, а значение температуры, измеряемой на оси дуги, приводится всегда. Сравнение измеренных значений осевой температуры To со средними ее значениями <To> в канале аргоновых дуг как измеренными, так и рассчитанными по формуле (7), показало постоянство этого отношения для режимов с малыми потерями на излучение. Средняя величина отношения θ=To/<T> равна <θ>=1,12. Фактические значения осевой температуры отклоняются от этого значения в большинстве случаев не более, чем на ± 0,05. Это иллюстрирует таблица 1. Данные таблицы [14, 16] относятся к свободногорящим дугам, остальные к дугам, стабилизированным холодными стенками. В случае свободногорящих дуг радиус канала R считался (за неимением ничего лучшего) равным наблюдаемому световому диаметру канала.
Здесь уместно пояснить следующий момент. В дугах, в которых канал разряда не ограничен стенками, то есть свободногорящих, радиус канала R является внутренним параметром, зависящим от тока, давления и рода газа. Если мы принудительно ограничиваем канал разряда стенками (например, формируем его в трубке), то радиус канала становится внешним параметром, уже зависящим от нашего произвола. Вероятно, радиус канала свободно горящей дуги при выбранных значениях тока и давления является тем значением, ниже которого радиус канала ограниченной стенками дуги становится внешним параметром. К чему это сказано? А вот к чему. Если значение θ начинает существенно превышать среднее значение (например, становится равным 1,20), то это означает, что канал разряда не заполняет сечение разрядной трубки, при этом формула (7) дает заниженное значение T. Это означает, что радиус канала разряда существенно отличается от радиуса разрядной рубки.
С другой стороны, если величина θ занижена (например, равна 1,03) в тех случаях, когда радиус канала близок по величине к радиусу ограничивающей трубки, то это означает, что при данном режиме велика доля излучательных потерь f=W(W+Q)-1. Действительно, в опытах 18 и 20, приведенных в таблице, доля излучательных потерь f составляет 65-85%. Если это учесть, то величина θ для этих случаев будет близка к величине 1,12. Очевидно, что введенная ранее величина δ связана с f соотношением δ=f(1-f).
Определение температуры в дуге с помощью формулы (7) сильно упрощается, если зависимость (8) представить в виде графика (рис. 3), на котором по оси ординат отложены значения модельной (средней) температуры в канале, а по оси абсцисс значения lgB(T).
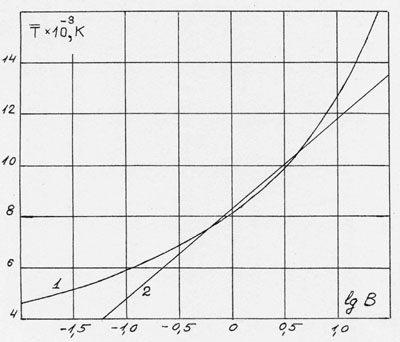
Рис.3. График, связывающий значения T и lgB(T) в аргоновых каналовых дугах, взятый из работы [7], изображен на рисунке кривой 1. Прямая линия 2 представляет собой аппроксимацию зависимости 1 в области температур 7000– 11000K.
Для определения величины средней температуры в канале дуги с заданными значениями тока, радиуса и давления рассчитывается логарифм B(T) выражения (7). После этого среднее значение температуры в канале определяется по кривой 1, изображенной на рисунке. Как видно, процедура определения температуры не сложная.
В качестве примера рассчитаем температуру аргоновой дуги атмосферного давления, проанализированной в начале этой страницы. Ток дуги 60 А, радиус канала 0,032 м. Подставим значения этих величин в правую часть выражения (7) и определим численное значение величины B(T). Найдя логарифм полученного численного значения, определим затем по графику на рис. 3 величину средней температуры в канале. Упомянутая процедура приводит в рассматриваемом случае к значению средней температуры, равному 9900К. С учетом упомянутого выше эмпирического отношения температура на оси будет в 1,12 раза превышать среднюю и равняться в данном случае 11100К. Это значение хорошо согласуется со скорректированным значением температуры на рис. 2. Таким образом, получаем еще одно подтверждение справедливости представления о канале дуги, как потенциальной яме. Здесь попутно отмечу следующее, зависимость (7) калибровалась по данным, относящимся к аргоновым дугам, канал которых стабилизирован водоохлаждаемыми медными шайбами. А в данном примере она была использована для определения температуры в дуге, канал которой стабилизирован кварцевой водоохлаждаемой трубкой. Это указывает на то, что средняя температура в дуге слабо зависит от внешних условий.
Приведенные результаты говорит в пользу, работоспособности выражения (5), а точнее исходного представления о потенциальной яме. На активной стадии исследований был накоплен большой экспериментальный материал, подтверждающий выражение (5), но, к сожалению, опубликовать его в свое время не удалось. Для далеко не полной иллюстрации работоспособности (5) выше приведена ссылка на таблицу 1 с экспериментальными и рассчитанным по формуле (7) значеними температуры при различных режимах каналовых дуг, в том числе горящих и при давлениях выше атмосферного. Привожу упомянутую ссылку вторично. В дополнение привожу таблицу 2 [7]. В этой таблице работоспособность формулы (7) демонстрируется на примере импульсных аргоновых ламп, работающих при токах до 2000 А. В дальнейшем надеюсь проиллюстрировать работоспособность (7) на других более убедительных, содержащих саму по себе ценную информацию, примерах. Сейчас я этого не делаю, чтобы не выходить за пределы разумных размеров страницы.
Пояснение по поводу депонированной работы 1989 г. [7]
Здесь уместно сделать пояснение по депонированной работе [7], чтобы был понятен приведенный в ней вывод зависимостей для сильноточного разряда и, в частности, зависимости (7). Это необходимо потому, что представителем редколлегии (см. страницу «История исследования») было предложено переработать первоначальный вариант работы, убрав из нее предлагаемую интерпретацию приведенного обширного экспериментального материала, построенную на представлении о канале разряда, как о «потенциальной яме». Как мне сейчас представляется тогдашняя ситуация, дело обстояло следующим образом. Согласно существующим устоявшимся представлениям вклад в теплопроводность плазмы поляризационных процессов незначителен. Поэтому говорить о них не имеет смысла. С другой стороны, экспериментирование с разрядом привело меня к прямо противоположному выводу, что, наоборот, именно поляризационные процессы играют главную роль в энергетике разрядов. Но эта точка зрения не была поддержана, и мне пришлось переделать статью. При переработке статьи использовать явно выражение для величины снижения энергии ионизации я уже не мог. А без него, как показано на странице «Роль поляризации плазмы», невозможно получить выражение температуры в канале через внешние параметры. Это связано с тем, что только для этого выражения (см. формулу (1)) известна связь температуры с параметрами плазмы. Поэтому, чтобы обойти возникшее препятствие на пути публикации работы, пришлось заменить величину снижения энергии ионизации двумя другими специально введенными для этого величинами, которые неявным образом учитывали потенциальную яму в энергобалансе канала дуги.
- Вводим скачок температуры ΔT согласно соотношения:
χo=kΔT. (10)
- Зависимость k-1χo(T) на рис.1 аппроксимируем линейной функцией
в области температур, характерной для каналовых
аргоновых дуг (7000-12000К):
k-1χo=τo(T-Tc), (11)
где τo и Tc - постоянные.
- Перепишем выражение (11) в следующем виде:
χo=τkT, (12)
где τ=τo(1-Tc/T).
- На основе выражений (10) и (12) запишем:
ΔT=τT (13)
Отмечу, что непосредственно знать величину коэффициента τ еще недостаточно, потому что в выражение Ho, кроме всего прочего, входят еще эффективные сечения столкновения электронов с атомами и ионами, значения которых с требуемой точностью неизвестны. Поэтому получить в данной ситуации рабочую зависимость, пригодную для практических расчетов, удается только при определении значения Ho по экспериментальным данным. В случае аргоновых дуг единственное значение Ho перекрывает фактически весь изученный температурный диапазон этих дуг.
Вариант работы, при котором вместо величины χo использовалась величина τ, был депонирован в 1989 г. [7], а аннотация на него появилась в журнале ТВТ в 1990 г. [9]. Такая замена сделала работу малопонятной. Чтобы показать, что в основе ее заложено представление о канале разряда, как о своеобразной потенциальной яме, мною была написана другая работа, которую я первоначально направил в ЖТЭФ. Но ее очень быстро вернули обратно, как не представляющую интереса «для широкого круга» читателей журнала. Подредактировав эту работу, переправил ее в ТВТ. Через месяц из редакции ТВТ меня разыскали на работе по телефону и сообщили, что статья запускается в набор и нужно срочно внести поправки в соответствии с замечаниями рецензента, так как решено напечатать ее в очередном номере. Для меня это была хорошая весть, так как появление этой статьи в печати открывало возможность для публикации на ее основе неизвестных ранее результатов, касающихся разрядов. Однако в текущем номере статья не появилась, редколлегия изменила свое решение. Добиться за полтора года сколько-нибудь вразумительных объяснений отказа я так и не смог (см. «История исследования»).
Краткое резюме
На этой страничке я пытаюсь в очередной раз за прошедшие 30 лет привлечь внимание к роли поляризации плазмы в канале сильноточных разрядов. Здесь эта роль продемонстрирована при токах разряда порядка десятков и сотен ампер, но проведенные эксперименты указывают на ее ведущую роль и при бóльших значениях токов разряда, по предварительным данным, - порядка десятков и сотен килоампер.Л И Т Е Р А Т У Р А
- Griem H.R. //Phys. Rev. 1962. V. 128. No.3. P. 997-1006.
- Физика и техника низкотемпературной плазмы. Под ред. Дресвина С.В. М.: Атомиздат, 1972. 352 с.
- Райзер Ю.П. Физика газового разряда. М.: Наука, 1987. 592 с.
- Knopp C.F., Cambel A.B. //Phys. Fluids. 1966. V.9. No. 5. P.989-996.
- Батенин В.М., Минаев П.В. //ТВТ. 1969. Т. 7. № 2. С. 208- 212.
- Bott Y.F. //Phys. Fluids.1966. V. 9. No. 8. P. 1540-1547.
- Пышнов А.В. К вопросу построения модели канала квазистационарной сильноточной ограниченной стенками дуги. М.: Деп. ВИНИТИ № 6889-В89.1989. 35 с.
- Пышнов А.В. //ТВТ. 1978. Т. 16. № 5. С. 914-921.
- Пышнов А.В. //ТВТ. 1990. Т.28. № 2. С.410.
