КАНАЛОВАЯ МОДЕЛЬ ЭЛЕКТРИЧЕСКОЙ ДУГИ
Введение
На предыдущей странице "Роль поляризации..." показано, как анализ экспериментальных данных, привел к выводу, что неизлучательные потери энергии из канала электрического сильноточного квазистационарного разряда определяются в основном поляризационными процессами в плазме канала. Этот результат явился новым и совершенно неожиданным, впервые он был неявным образом использован в работе [1, 2] для анализа энергобаланса электрических квазистационарных разрядов как с преобладанием излучательных потерь энергии из разряда, так и без таковых.
Здесь упомянутый анализ выполнен более подробно, чем в работе [2], для разрядов без преобладания излучательных потерь энергии. Типичными представителями таких разрядов являются электрические дуги, горящие при давлениях порядка атмосферного или выше.
Учет поляризационных процессов позволяет по-новому решить задачи, касающиеся как зависимости температуры канала дуги от внешних параметров, так и расчета вольтамперных характеристик дуг (как свободно горящих, так и стабилизированных стенками).
Чтобы наглядно увидеть разницу в решении названных задач с помощью нового подхода, учитывающего поляризацию плазмы канала, и традиционного, корни которого уходят к тридцатым годам прошлого века, напомним сначала суть последнего.
1. Классическая каналовая модель.
1.1 Уравнение Эленбааса-Хеллера (1934 г.)
Уже в тридцатых годах прошлого столетия на основе теоретических и экспериментальных работ сформировалось представление, что в столбе дуг высокого давления с достаточно хорошим приближением реализуется состояние термической плазмы. Под этим термином подразумевается, что все основные процессы в такой плазме являются однозначными функциями температуры, одинаковой для всех плазменных частиц. На основе этого Эленбаасом и Хеллером была предложена теория столба дуги, которая послужила основой для последующих теорий. Проведем элементарный вывод основного уравнения этой теории, описывающего баланс энергии в плазме разряда.
Предварительно оговорим исходные условия. Анализируем однородный по длине цилиндрический столб дуги в продольном электрическом поле, напряженность которого Е. Считаем, что дуга горит в неподвижном газе, находящемся при постоянном давлении в охлаждаемой трубке радиуса Rt. Рассматриваем режимы, при которых излучательные потери энергии из столба малы, а потери энергии из столба определяются в основном процессами теплопроводности в столбе дуги.
Как известно, тепловой поток в среде
описывается выражением
Здесь J - удельный тепловой поток, λ - коэффициент теплопроводности, Т - температура.
В силу допущенной однородности столба по длине и его цилиндрической симметрии все параметры вещества в столбе являются функциями только текущего радиуса столба r. В частности, градиент температуры в этом случае представляет собой производную от температуры по радиусу, то есть в столбе реализуются лишь радиальные потоки тепла.
Чтобы записать дифференциальное
уравнение, описывающее связь между параметрами столба, проанализируем
энергобаланс тонкого цилиндрического слоя столба радиуса r и
толщины Δr. Для упрощения записи выкладок рассмотрим энергобаланс
цилиндрического слоя в расчете на единицу его длины. Очевидно, что
энергобаланс слоя складывается из следующих частей: входящего теплового
потока Q+ через внутреннюю стенку слоя радиуса r;
тепловой энергии QE, генерируемой в слое протеканием
тока, и выходящего теплового потока Q- через наружную
стенку слоя радиуса r+Δr. В итоге баланс запишется в виде:
Раскроем выражения, входящие в энергобаланс.
Входящий тепловой поток представим в виде:
Мощность тепловой энергии QE , генерируемой в цилиндрическом слое за счет протекания тока, запишем как:
где σ(r) - удельная электропроводность среды в слое радиуса r.
Величину Q- выразим следующим образом:
Подставляя
выражения (3-5) в уравнение энергобаланса (2), прийдем после
элементарны преобразований полученного выражения к дифференциальному
уравнению, которое, обычно, записывается в виде:
Это и есть известное уравнение Элеенбаса-Хеллера. Граничные условия для него: на оси столба (r=0) производная dT/dr=0 вследствие симметрии, при r = Rt температура T = Tt , где Tt - температура стенок трубки.
1.2 Каналовая модель дуги (1932 г.). Принцип минимума Штеенбека.
Решить уравнение (6) в общем виде аналитически не удалось до настоящего времени. Однако разрабатывались различные приближенных методы его решения [3].
В частности, известен метод приближенного решения этой задачи, основанный на учете качественного различия разных областей дуги. Эти различия отражены в хорошо известной каналовой модели дуги, предложенной Штеенбеком в 1932 г., то есть еще до установления уравнения (6). Данная модель учитывает тот факт, что электропроводность плазмы очень сильно зависит от температуры.
Температура в столбе дуге спадает от оси к стенкам, поэтому основная часть
тока протекает в приосевой области трубки, где температура наиболее
высокая. Поэтому в предложенной модели столб дуги делят на зону
проводимости диаметром 2R с постоянным значением температуры
Т и зону потерь энергии, температура которой изменяется от величины
Т до Тt - температуры стенок, окружающей столб
трубки. Причем в зоне потерь энергии считается, что электропроводность
вещества равна нулю, то есть ток через эту зону не
течет.
Протекание тока через центральную зону
каналовой модели описывается законом Ома:
При постоянной силе тока дуги I и заданной температуре стенок трубки Tt это выражение связывает между собой три переменные величины T, R и E.
Чтобы получить еще одно независимое выражение, связывающее эти величины, проинтегрируем уравнение (6) в бестоковой зоне каналовой дуги, учитывая, что в этой зоне σ=0. Интегрирование показывает, что величина
rJ(r) постоянна в этой зоне, что само по себе очевидно, кроме того,
она равна:
Это
следует из того, что электрическая мощность, выделяемая в канале, равна
IE, поэтому тепловой поток на границе R равен
IT/2π.
Замена в (8) величины потока J его явным
выражением -λdT/dr приведет к нелинейному дифференциальному
уравнению, но эту трудность удается обойти, путем введения функцию:
Эта
функция обладает тем свойством, что производная от нее, как легко видеть,
равна тепловому потоку J, взятому с обратным знаком:
Из сравнения выражений (8) и (10) вытекает легко интегрируемое дифференциальное уравнение:
Интегрирование обеих частей этого выражения от Rt до R приводит к следующему уравнению, связывающему величины I, T и R:
Таким образом, мы имеем два уравнения (7) и (12), которые при заданной силе тока I и заданных условиях окружающей среды (T=Tt при r=Rt) связывают три переменные T, r и E. Исключая из этих выражений одну из переменных, например, переменную T, получим бесконечную последовательность режимов горения дуги выражаемую функциональной зависимостью E (r).
Чтобы из
указанной последовательности режимов можно было выбрать тот, который
фактически реализуется, используется допущение, известное как минимальный
принцип Штеенбека. Согласно этому допущению при заданной силе тока и
фиксированных условиях окружающей среды реализуется тот режим, при котором
напряженность электрического поля минимальна. Другими словами при этом
режиме производная
Принцип Штеенбека был не раз проверен при исследовании дуговых разрядов. При этом были получены результаты, удивительно хорошо согласующиеся с экспериментом [4]. Однако вопрос обоснования этого принципа не перестает волновать исследователей до настоящего времени.
Подводя итоги,
можно сказать , что каналовая модель позволяет рассчитать температуру и
напряженность поля в дуге. Однако эти расчеты сложны, поэтому
имеются расхождения между данными разных авторов. Ведь при расчете
теплопроводности λ(Т) плазмы приходится учитывать большое
количество процессов, поскольку она складывается из величин
теплопроводности молекул (в случае молекулярных газов), атомов, ионов,
электронов; кроме того, нужно учесть также вклад от диффузии энергий
ионизации и диссоциации.
Учет всех этих процессов
приводит к сложной зависимости теплопроводности плазмы λ(T) от
температуры. На рис.1 представлена для иллюстрации типичная зависимость
теплопроводности от температуры [3, 5], скопированная из [5]. Здесь
же изображена функция Θ(Т). Видно, что за счет интегрирования эта функция
существенно «глаже», чем функция теплопроводности. Ее приближенно можно
аппроксимировать отрезком прямой линии.
Отметим в заключение раздела основные особенности классической
каналовой модели дуги, следующие из приведенного краткого ее описания.
Во-первых, в этой модели токовый канал рассматривается как цилиндрический
однородный бесструктурный оммический нагреватель c погонной мощностью EI, имеющий температуру T.
Во-вторых, основную роль в ней играют процессы теплопроводности в газообразной фазе бестоковой зоны столба дуги.
В-третьих, из каналовой модели вытекают два соотношения, связывающие три неизвестные величины, характеризующие канал дуги: T, E, R, которые следует определить. Чтобы однозначно определить эти величины, требуется третье соотношение, связывающее эти величины. Однако непосредственно такое соотношение из классической модели не вытекает.
Поэтому для получения недостающего соотношения Штеенбеком был сформулирован принцип минимума, который непонятно как связан с каналовой моделью, но применение которого, тем не менее, приводит к хорошему согласию модельных вольтамперных характеристик канала дуг с экспериментальными.
В заключение хочу напомнить, что электрическая дуга является преобразователем электрической энергии в световую (излучательную) и тепловую. Для технических применений важно знать энергетические параметры дуги и, в первую очередь, величину поглощаемой ею электрической мощности. Поэтому одной из задач, которые следовало для этого решить, была, в частности, задача научиться рассчитывать вольт-амперную характеристику проводящего канала дуги. Техническая потребность в этом и привела к разработке классической модели каналовой дуги.
На этом я хочу закончить
рассмотрение классической каналовой модели и перейти к следующему разделу.
2. Модернизированная каналовая модель, учитывающая поляризацию плазмы.
2.1 Энергобаланс однородного гипотетического канала дуги с учетом поляризации.
Плазма представляет собой ионизованный квазинейтральный газ.
Квазинейтральность означает, что число положительных и отрицательных зарядов в плазме
одинаково. Дальнодействующее кулоновское взаимодействие заряженных частиц приводит
к целому ряду качественных особенностей плазмы, отличающему ее от обычного газа,
в котором нет заряженных частиц. Это дает основание считать плазму особым, "четвертым"
состоянием вещества. Таким образом, вещество, согласно сказанному, может находиться в
твердой, жидкой, газообразной и плазменной фазе. Причем переход вещества из одной фазы в другую происходит с ростом температуры.
Наличие в плазме свободных электрических зарядов приводит к так называемым плазменным поляризационным эффектам, которые, в частности, проявляются в том,
что такие энергетические параметры вещества как энергия ионизации частиц и кулоновская энергия заряженных частиц оказываются в плазменной фазе заниженными по сравнению с аналогичными параметрами частиц, находящихся в газообразной фазе. Поэтому при физическом контакте плазменной и газообразной фазы между ними существует энергетический барьер, который, с одной стороны,
благоприятствует перемещению частиц из газовой фазы в плазменную, а, с другой стороны, требует затраты энергии на преодоление этого барьера, при перемещении частицы обратно из плазменной фазы в газовую.
Электрическая дуга состоит из плазменного канала, по которому протекает ток, и окружающей его оболочки (так называемой "шубы") из нейтрального газа. Здесь налицо контакт двух фаз, на границе которых существует энергетический барьер. Анализ экспериментальных данных, частично проведенный на опубликованных ранее страницах сайта, приводит к выводу, который можно сформулировать следующим образом. Электрическая мощность P=EI, поглощаемая каналом в расчете на единицу его длины, расходуется, во-первых, на излучательные потери энергии W, а, во-вторых,
на неизлучательные Õ, обуславливаемые необходимостью удалять частицы, поступающие в канал из оболочки, для сохранения стационарности последнего.
Это уравнение энергобаланса, записанное для зоны проводимости каналовой модели с учетом поляризации плазмы, является третьим уравнением, связывающим между собой величины T, E и R каналовой модели. Подробно это уравнение раскроем и проанализируем чуть позже, а сначала обсудим общие вопросы, связанные с этим уравнением.
Установление третьего уравнения позволяет отказаться от принципа
минимума Штеенбека, который, вообще говоря, никак не следует из классической каналовой модели. В свое время это вызвало многочисленные дискуссии [4], которые здесь рассматривать не будем, а обсудим принцип с новых позиций, учитывающих поляризацию плазмы канала.
На перемещение частицы через энергетический барьер из плазменной в нейтральную фазу требуется сообщить частице энергию не меньше, чем величина этого энергетического барьера. Если предположить, что на каждую удаляемую частицу расходуется энергия практически не превышающая минимального значения, то это означает, что для поддержания плазменного канала в стационарном состоянии тратится минимально необходимая мощность Õ. Согласно сказанному выше, эта величина близка к величине EI, если излучательные потери W малы, что обычно выполняется в дугах атмосферного давления. Это, в свою очередь, означает, что при фиксированном значении тока I величина напряженности поля E в плазменном канале минимальна.
Таким образом, предположение о том, что на удаление частицы из канала расходуется минимальная энергия, приводит к принципу минимума на основе учета поляризационных свойств плазмы. Поэтому можно сказать, что принцип минимума Штеенбека неявным скрытым образом учитывает наличие на границе зоны проводимости энергетического барьера, о существовании которого не было известно более семидесяти лет, хотя первая робкая попытка с моей стороны обратить на это внимание на страницах журнала "Теплофизика высоких температур", закончившаяся отказом, была предпринята еще в 1976 г..
С другой стороны, обратное предположение, сделанное на основе принципа минимума Штеенбека, согласно которому дуга горит при минимальной напряженности электрического поля, приводит к выводу, что на поддержание дуги расходуется минимальная электрическая мощность, а, следовательно, тратится минимальная мощность для удалении частиц из канала через энергетический барьер.
Таким образом, видно, что из одного допущения вытекает другое и наоборот. Это не позволяет однако строго доказать ни одно из них, но позволяет понять, как принцип минимума Штеенбека связан с каналовой моделью.
2.2 Аналитическое выражение для температуры однородного канала.
Найдем аналитическое выражение для модельной температуры канала дуги через ее внешние параметры. С этой целью раскроем уравнение энергобаланса для центральной зоны модели каналовой дуги (14). Чтобы избежать работы с громоздкими выражениями, выкладки проведем для каналовых дуг, горящих в атмосфере газов, состоящих только из одного химического элемента (аргон, азот, кислород и т.д.). Рассмотрение ограничиваем режимами, при которых плазма канала состоит из атомов, однократно заряженных ионов и электронов с концентрациями, равными, соответственно, no, n1 и ne, причем в силу квазинейтральности плазмы ne=n1. Напомним, что, по определению, температура T в центральной зоне модели постоянна. Выкладки проводим для канала единичной длины.
С учетом сказанного величину мощности P, подводимую к каналу, представим, используя выражение (7), в следующем виде:
Величина излучаемой каналом дуг мощности W для широкого диапазона режимов достаточно незначительна, поэтому при анализе энергобаланса дуг не слишком высокого давления ею пренебрегают. Мы этого делать не будем, но, так как аналитическое выражения для этих потерь не известно, то учтем эти потери формально. Учет потерь выполним с помощью введения множителя δ согласно соотношения:
Перепишем уравнение энергобаланса (14) с учетом формул (15-16) в виде, удобном для проведения дальнейших преобразований:
Выражение для мощности поляризационных потерь (МПП), которое на этой странице обозначено буквой Õ вместо использовавшейся на других страницах буквы Q, сразу запишем в окончательном виде, вытекающем из общей формулы (2) на странице "История исследования..." при раскрытии ее с помощью выражений (9-15) на той же странице:
Символы K1 и α в этой формуле обозначают комбинации физических параметров, причем численные значения всех комбинаций на данной странице сайта даны в системе МКСА:
Записанное выражение учитывает то обстоятельство, что порции энергии, затрачиваемые на удаление за пределы канала атомов, ионов и электронов, различаются между собой множителем порядка двойки. В более раннем варианте работы [2] этим различием пренебрегалось.
Напомню смысл некоторых приведенных здесь символов.
Символом ψ обозначено отношение величины скорости электронов в плазме к скорости тяжелых частиц (атомов и ионов). Символом η обозначена степень ионизации плазмы, записанная в приведенном виде с учетом ее малости в электрических дугах. Величина τ показывает (с точностью до множителя 2/3), какую долю составляет величина снижения энергии ионизации атомов в плазме χo от величины поступательной энергии kT частиц плазмы. Величина τ возрастает с температурой плазмы до определенного предела, а затем начинает уменьшаться при условии, что давление в плазмы постоянно. Это можно, например, увидеть из "графика зависимости" χo(T) для аргоновой плазмы, приведенном на странице "История исследования" этого сайта.
Выразим удельную электропроводность σ плазмы, входящую в энергобаланс (15), через другие параметры плазмы канала. Согласно общеизвестной формуле ее связь с другими параметрами плазмы описывается выражением:
Здесь e - заряд электрона, λe - длина свободного пробега электронов, Qeo и Qe1 -эффективные сечения столкновений электронов с атомами и ионами [4]. Через величину Qef обозначена комбинация величин:
При записи (23) учтено, что в слабо ионизованной плазме величина n1no-1 практически равна степени ионизации плазмы η.
С учетом физики процессов, определяющих электропроводность плазмы, дуги удобно разделить на низкотемпературные, когда σ зависит, в основном, от столкновений электронов с атомами, среднетемпературные, когда σ определяется столкновениями электронов с ионами, и высокотемпературные, когда σ перестает зависеть от степени ионизации плазмы и зависит только от температуры. Высокотемпературные дуги на этой странице рассматриваться не будут, это уже сделано на странице "История исследования...".
Запишем рабочее выражение для σ. С этой целью выразим концентрацию электронов в плазменном канале через концентрацию атомов и температуру плазмы с помощью уравнения Саха [6]:
Здесь Z1 и Zo - статистические суммы ионов и атомов, h - постоянная Планка, Eo - потенциал ионизации атомов.
В силу квазинейтральности плазмы концентрации электронов и ионов в ней совпадают, то есть ne=n1. Поэтому, умножив обе части уравнения Саха на no и извлекая из них квадратный корень, получим выражение для концентрации электронов ne.
Подставив полученное выражение в формулу (21) и сгруппировав символы в получившемся выражении, прийдем к следующей рабочей формуле для удельной электропроводности плазмы:
Для записи зависимости температуры канала в удобном виде используем вместо величины концентрации атомов в канале no величину давления p, при котором горит дуга. Давление связано с концентрацией законом Дальтона; с учетом малой степени ионизации плазмы в дугах, а также полной диссоциации молекул в канале в случае молекулярного плазмообразующего газа можно приближенно записать:
Подставив выражения (18) и (25) в (17), учтя (26) и извлекши квадратный корень из обеих частей записанного выражения, сгруппируем множители, в него входящие, следующим образом. В одной части до знака равенства оставим множители, в которые явным образом входит температура T, а в другой части разместим все остальные множители. Для удобства работы полученное выражение разобъем на два отдельных. Для этого каждую его часть приравняем одному и тому же выражению B(T). В результате получим искомую зависимость, связывающую T c I, R, p и параметрами вещества, в следующем виде:
Через F в (29) обозначена комбинация:
Для полноты картины запишем в явном виде выражение для величины Fo, используя зависимости (20) и (23):
Обсудим приемы работы с полученной зависимостью (27-31). Из рассмотрения выражения (28) следует, что величина B(T) зависит только от температуры, но реально это не совсем точно, поскольку энергия ионизации атомов в плазме равна не Eo, а величине Eo-χo, которая уже зависит и от давления плазмы p. Однако, вклад этой поправки незначителен и ею можно пренебречь.
Величина H (29) зависит косвенно от температуры и давления, в связи с этим выражение (27) перезапишем в ином виде, учитывающем это обстоятельство, а именно:
Для дуги, горящей при заданном давлении среды p, левая часть выражения (32) рассчитывается аналитически. Этот расчет удается полностью выполнить для значений давления p, при которых излучательные потери из канала дуги малы (δ<< 1). Затем строится вспомогательный график зависимости температуры T от логарифма lg(BH-1p1/4) левой части выражения (32).
Процедура расчета температуры на основе выражения (32) сводится к следующему. Сначала находится величина логарифма lgIR-3/2 для выбранных значений тока I и радиуса канала R, а затем по построенному вспомогательному графику определяется величина температуры.
По поводу радиуса канала отметим, что в каналовых дугах, горящих при значительных токах, радиус канала R совпадает практически с радиусом ограничивающего канала Rt. В этом случае привлекать уравнение (12) не требуется.
В частном случае, когда величину H можно считать постоянной, требуется построить график зависимости температуры T лишь от величины логарифма lgB(T) (28) и использовать непосредственно выражение (27). График T=T(lgB(T)) удобно построить в следующем виде: по оси ординат откладываются значения температуры T, а по оси абсцисс логарифм величины B(T), рассчитанной по формуле (28).
Для аргоновой дуги атмосферного давления этот график из [2] изображен на следующем рисунке (кривая 1).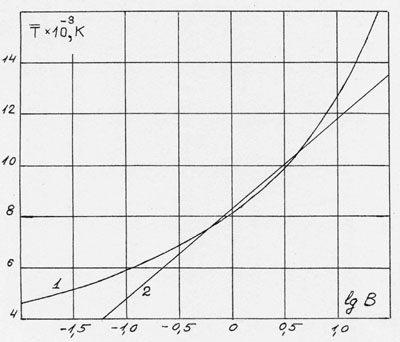
3. Сопоставление модельной зависимости для температуры с экспериментальными данными по аргоновым дугам.
3.1. Сравнение с экспериментальной зависимостью.
Чтобы записать формулу (27) для конкретного плазмообразующего газа нужно знать сечения столкновения электронов с атомами и ионами этого газа, необходимые для расчета зависимости H(T). Литературные сведения о величинах этих сечений, как будет проиллюстрировано ниже на примере аргона, характеризуются большим разбросом. Поэтому решено было оценить величину H(T), исходя из известных экспериментальных зависимостей. В качестве одной такой зависимости была проанализирована зависимость для средней электронной температуры в аргоновых каналовых дугах атмосферного давления, из [7]. Ниже приведено отсканированное изображение этой зависимости.

Эту графическую зависимость можно представить в следующем аналитическом виде:
Сравнение модельной зависимости (27) с эмпирической (33) показало, что, во-первых, величину H, в первом приближении, можно считать постоянной. Во-вторых, из анализа графика зависимости T=lgB(T), изображенного выше, следует, что для обеспечения погрешности расчета температуры около 3% необходимо, чтобы величина Qef, была известна с точностью 26% в области температур около 12000K и 47% в области температур около 7000K. В результате компромиса было выбрано постоянное значение H=1,62· 10-4. Логарифм этого значения lgH=-3,79 [2]. При таком выборе значения H результаты определения величины температуры T по модельной зависимости (27) практически совпадают с расчетными значениями, даваемыми эмпирической зависимостью (33), в области температур T от 7000 до 11500K, причем модельная зависимость оказывается работоспособной в значительно более широком диапазоне режимов [1], чем (33). В частности, модельная зависимость отражает зависимость температуры от давления, чего не делает зависимость (33).
3.2. Оценка эффективных значений величин сечений Qeo и Qe1 на основе экспериментального значения величины lgH.
Чтобы рассчитать модельное значение величины H по формуле (29), необходимо знать зависимости для сечений столкновения электронов с ионами и атомами Qe1 и Qeo от температуры. Однако эти зависимости точно не известны. Теоретические расчеты сечений, выполненные разными авторами, существенно различаются. Известные расчеты сечений приведены на сводном графике из [3]. Поэтому представляет интерес оценка величины сечений, исходя из экспериментального значения lgH=-3,79.
Для проведения оценок понадобятся следующие данные: плазмообразующий газ - аргон, относительный атомный вес - μ=40, энергия ионизации - Eo=15,7 эв, значения статистических сумм - Z1=6 и Zo=1. Кроме того, понадобятся: термодинамический состав плазы аргона, взятый из [5], и график k-1χo (рис.1) со страницы "Энергобаланс аргоновой дуги" этого сайта. Последний необходим для определения величины τ.
Полагаем также, что для случая дуг атмосферного давления долей излучательных потерь можно пренебречь, то есть считать , что δ=0.
Формулу (29) перепишем в следующем рабочем виде:
Согласно этой формуле экспериментальному значению lgH=-3,79 соответствует величина Fo= 8,55· 10-18. Исходя из выражения (30) для Fo=Qefα-1, оценим величину сечений при различных значениях температуры.
Оценки сечений представлены в таблице. В первых столбцах ее приведены термодинамические значения величин no, ne, τ, η и α в плазме канала
при различных значениях температуры
| 1,05· 1024 | 2,72· 1020 | 0,94· 10-2 | 2,59· 10-4 | 9,79· 10-3 | 8,40· 10-20 | ||
| 9,15· 1023 | 1,45· 1021 | 1,56· 10-2 | 1,58· 10-3 | 1,90· 10-2 | 1,0· 10-16 | ||
| 8,95· 1023 | 5,34· 1021 | 2,66· 10-2 | 5,97· 10-3 | 4,85· 10-2 | 6,9· 10-17 | ||
| 7,04· 1023 | 1,51· 1022 | 4,00· 10-2 | 2,14· 10-2 | 15,8· 10-2 | 6,6· 10-17 | ||
| 5,97· 1023 | 3,46· 1022 | 5,17· 10-2 | 5,80· 10-2 | 4,67· 10-1 | 6,8· 10-17 | ||
| 4,80· 1023 | 6,66· 1022 | 6,50· 10-2 | 13,9· 10-2 | 13,1· 10-1 | 8,0· 10-17 |
Результаты таблицы показывают, что оценки дают в несколько раз большие значения величины сечений Qe1 по сравнению с известными расчетами. Как это объяснить, пока не ясно. На полученной зависимости этого сечения от температуры четко просматривается влияние эффекта Рамзауэра.
3.3. Вольтамперная характеристика каналовой аргоновой дуги.
Как уже упоминалось, что, если канал дуги ограничен охлаждаемыми стенками, а величина тока велика, то радиус плазменного канала практичеки совпадает с радиусом ограничивающего канала. В этом случае формула (27) позволяет рассчитать величину средней температуры канала T. Если известна зависимость удельной электропроводности плазмы от температуры, то для упомянутых режимов можно легко рассчитать величину напряженности поля в дуге, то есть вольтамперную характеристику канала дуги. Однако выполнение этого простого расчета упирается в отсутствие надежных сведений о электропроводности плазмы, так как напряженность электрического поля очень чувствительна к этой величине. На следующем рисунке представлены известные экспериментальные данные и расчетные зависимости электропроводности аргоновой плазмы, выполненные разными авторами.
Видно, что данные характеризуются значительным разбросом, поэтому не ясно, какие из них можно использовать для точных расчетов.
Чтобы выяснить это, автором сайта были проанализированы экспериментальные вольтамперные характеристики каналовых аргоновых дуг атмосферного давления, стабилизированных водоохлаждаемыми стенками. На следующем рисунке приведены результаты измерения напряженности электрического поля в дугах, взятые из [8]. Диаметр стабилизирующего канала в случаях 1, 2 и 3 равен соответственно 4; 6 и 8 мм. Значения поля E получены из распределения потенциала вдоль дуги и из вольтамперных характеристик дуг различной длины (светлые треугольнички).
На основе этих данных по известным из условий опытов значениям тока и диаметра каналов, а также измеренным значениям напряженности электрического поля были рассчитаны для каждого режима средние значения электропроводности плазмы и значения модельной температуры по формуле (27), причем при расчете использовалось эмпирическое значение lgH=-3,79. В результате было установлено, что значения электропроводности, найденные из обработки экспериментальных данных в зависимости от модельной температуры, хорошо согласуются с теоретической расчетной зависимостью, которая получена в работе [9]. Это иллюстрирует следующий рисунок, на котором представлены полученные экспериментальные значения электропроводности и теоретическая зависимость [9], помеченная буквой D. На рис. 2.7 эта теоретическая зависимость изображена штрих-пунктирной кривой.
Отсюда следует, что появилась возможность проведения прямого и быстрого расчета вольтамперных характеристик. Этот результат является еще одним аргументом в пользу развиваемой модели. На этом я и хочу пока закончить эту страницу. Надеюсь, что представленный материал еще раз подчеркнет основную мысль, проводимую на сайте, что существенную роль в сильноточных электрических разрядах играют поляризационные плазменные процессы, на что я пытаюсь обратить внимание с 1976 г.
Написано 31 марта 2006 г.
Проведена перегруппировка материала последнего раздела 03 апреля 2006 г.
- Пышнов А.В. //ТВТ. 1990. Т. 28. № 2. С. 410.
- Пышнов А.В. К вопросу построения модели канала квазистационарной сильноточной ограниченной стенками дуги. - М.: Деп. ВИНИТИ № 6889-В89 1989. 35 с.
- Физика и техника низкотемпературной плазмы. Под ред. Дресвина С.В. - М.: Атомиздат, 1972. 352 с.
- Финкельнбург В., Меккер Г. Электрические дуги и термическая плазма: Пер. с нем. / Под ред. Фабриканта В.А. - М. : ИЛ, 1961.
- Райзер Ю.П. Физика газового разряда. - М.: Наука, 1987. 592 с.
- Методы исследования плазмы. Под ред. В. Лохте-Хольтгревена - М. : "Мир", 1971.
- Клубникин В.С. Тезисы докладов У Всесоюзной конференции по генераторам низкотемпературной плазмы. Новосибирск, 1972. С.115-118.
- Асиновский Э.И., Кириллин А.В. //ТВТ. 1965. Т.3. № 4. С. 677.
- De-Voto R.S. //Phys. Fluids. 1967. V. 10. № 2.