ОПРЕДЕЛЕНИЕ ДАВЛЕНИЯ В СИЛЬНОТОЧНОМ РАЗРЯДЕ. МЕТОДИКА И ЕЁ
РЕЗУЛЬТАТЫ
Введение
Для измерения давления в разрядной трубке, в
которой формировались сильноточные разряды, был разработан, изготовлен и
отлажен пьезоэлектрический датчик давления.
Этот датчик первоначально
был откалиброван с помощью падающего шарика, который создавал
сосредоточенную нагрузку, поэтому было не ясно, годится ли такая калибровка
для точного измерения давления в разрядной трубке в условиях
распределенной нагрузки. В связи с этим значения давления, регистрируемые
этим датчиком в разрядной трубке, в течение продолжительного времени
рассматривались как относительные.
Чтобы произвести заведомо
абсолютную калибровку датчика, пришлось потратить более полугода. Такая
калибровка была выполнена после того, как возникли сомнения в возможности
использования известных спектроскопических методов диагностики плазмы для
исследования плазмы сильноточного многокилоамперного разряда, создаваемого
в небольшом замкнутом объеме, то есть в чрезвычайно экстремальных
условиях. Поэтому важно было понять, насколько можно доверять упомянутым
методам диагностики.
Здесь подробно рассмотрены этапы разработки
методики измерения давления в разрядной трубке, кратко рассказано о
результатах, полученных с ее помощью, при исследовании сильноточных
разрядов. Приведены также некоторые сведения о тех свойствах разрядов,
которые напрямую не касаются методики измерения давления, но существенны
для понимания некоторых ее методов.
1. ПЬЕЗОДАТЧИКИ
1. 1. Окончательный вариант конструкции пьезодатчика давления.
При отработке конструкции пьезодатчика было изготовлено несколько различных вариантов пьезодатчиков как без передающих стержней, так и с передающими. Сравнение их при проведении измерений давления в разрядной трубке однозначно заставило остановиться на пьезодатчике с передающим стержнем, способным стабильно работать в условиях высоких тепловых нагрузок. Чертеж разработанного датчика приведен на рисунке 30.
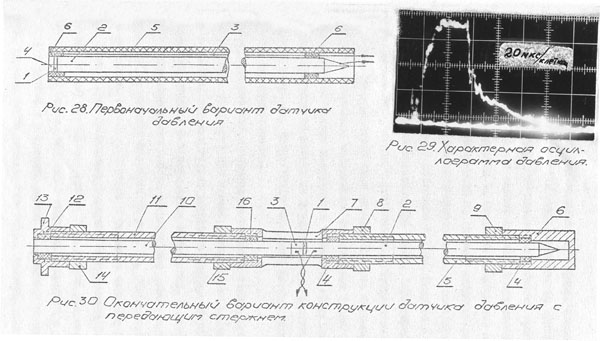
Основными элементами датчика являются: таблетка 1 из
пьезокерамики ЦТС-19, кварцевый передающий стержень 10, акустический
стержень 2, имевшие наружный диаметр 6 мм. Основная сложность при
изготовлении таких датчиков заключается в сборке, так как требуется
закрепить передающий и акустический стержни без возникновения паразитных
напряжений. В данном случае эту сложность удалось обойти за счет выбора
рациональной конструкции корпуса датчика.
Сборка датчика
осуществлялась следующим образом. Сначала к посеребренной с обеих сторон
таблетке 1 из пьзокерамики с помощью сплава Вуда припаивались акустический
стержень 2 и короткая (5 мм) проводящая секция 3 из латуни для снятия
сигнала с таблетки. Затем акустический стержень закреплялся в резиновых
кольцах 4 в трубке 5 с помощью нажимной гайки 6 и соединительной муфты 7,
которые после затяжки контрились контргайками 8 и 9.
Аналогичным
образом кварцевый передающий стержень 10, располагаемый в трубке 11,
зажимался в ней передним концом в резиновом кольце 12 с помощью фланцевой
гайки 13, которая затем контрилась контргайкой 14. После этого трубка 11
ввинчивалась в муфту 7 так, чтобы между задним концом кварцевого стержня,
смазанным эпоксидной смолой, и секцией 3 оставался зазор не более 0,1 мм,
и фиксировалась контргайкой 15. На кварцевый стержень при этом
предварительно надевалось резиновое кольцо 16.
После затвердевания
эпоксидной смолы датчик был готов к работе. Данная конструкция и способ
сборки обеспечивают отсутствие паразитных напряжений в стержнях. Для
снятия внутренних напряжений стержни отжигались. Датчик оказался
долговечным и весьма стабильным. При выбранной длине стержней (около 400
мм) с его помощью можно было регистрировать процессы продолжительностью до
160 мкс.
Как видно, конструкция не очень сложная: так, мой домашний
токарный станочек довольно легко справился с этой задачей, причем не
только с изготовлением металлических частей собственно датчика, но и
штампа для вырубки резиновых колец, используемых в датчике. Штамп
обеспечил изготовление колец точной геометрической формы, что заметно
улучшило свойства датчика.
1. 2. Калибровка пьезодатчика падающим шариком.
Одним из важных параметров, характеризующих состояние плазмы, является давление. В случае короткоживущей плазмы измерение давления удобно осуществлять с помощью пьезоэлектрического датчика. При воздействии давления p(t) на передающий стержень на выходе датчика возникает напряжение u(t), связанное с давлением выражением:
где k - коэффициент пропорциональности. Для
проведения количественных измерений датчик калибруют с целью определения
коэффициента пропорциональности k. Основная трудность при этом
заключается в проведении калибровки в условиях, близких к рабочим, потому
что не ясно, как величина k может зависеть от характера
нагрузки.
Первоначальная калибровка датчика была выполнена с
помощью падающего шарика в связи со своей доступностью, дешевизной и
малыми затратами времени на ее проведение.
При падении с
высоты h на плоскость торца передающего стержня датчика шарик к
моменту удара о плоскость приобретает количество движения равное величине
m(2gh)1/2, где m - масса шарика, g -
ускорение свободного падения, зависящее от местоположения на земном шаре
:). Причем при выполнении калибровки датчик устанавливается и закрепляется
строго вертикально.
Если удар шарика о плоскость торца происходит
упруго, то шарик отскакивает обратно на высоту h, причем в момент
отскока скорость шарика изменяется по направлению, но сохраняется по
величине. Таким образом, за время удара происходит изменение количества
движения шарика, равное величине 2m(2gh)1/2. При
проведении этой операции необходимо подобрать шарики достаточной
твердости, чтобы они были способны упруго отскакивать на высоту,
составляющую не менее 90-95% от высоты падения. Кроме того, торец
кварцевого передающего стержня следует хорошо отшлифовать и отполировать.
Как следует из второго закона Ньютона, изменение количества
движения шарика за время удара равняется импульсу силы, возникающей в
процессе удара шарика о плоскость. Предполагая, что сигнал напряжения
u(t) с датчика и сила F(t) пропорциональны друг другу, то
есть F(t)=k'u(t), запишем следующее равенство:
где ts -
продолжительность удара. Это выражение позволяет определить величину k'.
Действительно, величина интеграла от напряжения в (2) вычисляется по
снимку осциллограммы напряжения с датчика, а правая часть выражения (2)
известна из условий опыта.
Используя в опытах стальные шарики
разной массы и бросая их с различной высоты, можно было менять параметры
силы, действующей на стержень. На основе проведенных опытов было
установлено, что коэффициент k' не зависит от величины силы и от
точки приложения удара на торце передающего стержня. Таким образом,
проведенная калибровка датчика не вызывала сомнений в случае измерения
величины сосредоточенных нагрузок.
С помощью шарика была также
произведена оценка частотных свойств датчика. Время нарастания и спада
сигнала при ударе зависит от массы шарика. Исследование рабочего датчика
было проведено шариками, обеспечивающими нарастание и спад сигнала в
пределах от 5 до 40 мкс.
В проводимом исследовании разряда нужно
было измерять не величину сосредоточенной силы, а давление в плазме,
представляющее собой распределенную нагрузку. Между коэффициентами
k в (1) и k' в (2) можно установить связь, принимая
следующие допущения. Во-первых, допускаем, что при ударе в передающем
стержне формируется плоская звуковая волна. Во-вторых, считаем, что
величина силы, действующей во время удара, равна произведению величины
напряжения σ, возникающего в стержне при распространении плоской
звуковой волны, на величину площади поперечного сечения стержня
s и, в-третьих, допускаем, что давление p(t), приложенное к
датчику и численно равное σ(t), вызывает в стержне такую же
звуковую волну, что и удар. При этих условиях имеют место равенства:
Из этого выражения следует, что k=k'/s. Для
применявшегося пьезодатчика k=15,9 атм/в.
При использовании
перечисленных допущений было не ясно, как априорно оценить реальную
величину допускаемой в определении коэффициента k погрешности. Это
было сделано экспериментально путем сравнения калибровок пьезодатчика,
выполненных как с помощью падающего шарика, создающего сосредоточенную
нагрузку, так и калибровки его с помощью равномерно распределенного давления на
торце передающего стержня, о чем рассказано в следующем разделе.
1.3. Баллистический метод и калибровка пьезодатчика с его помощью.
Сущность метода сводится к измерению импульса количества
движения, получаемого поршеньком от плазмы за время ее существования.
Метод имеет несколько разновидностей, о некоторых из них будет рассказано
ниже. А сейчас рассмотрим основной вариант.
Импульс количества движения
P, сообщаемый поршеньку плазмой, измерялся устройством, показанным
на рис. 34.
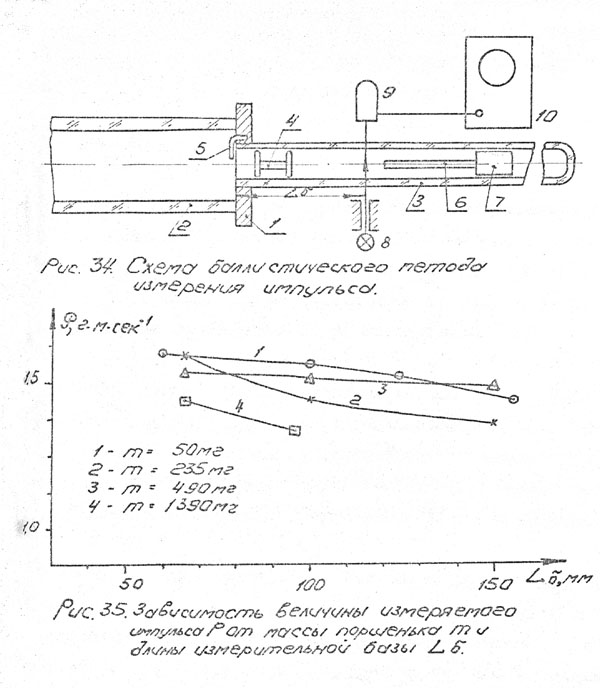
В центральном отверстии электрода 1 закреплялась своим
концом длинная (около 1 метра) горизонтально расположенная стеклянная
трубка 3 с внутренним диаметром 7,5 мм, запаянная на свободном конце. В
трубке свободно перемещался поршенек 4 диаметром 7,4 мм и длиной 10 мм.
Для фиксирования исходного положения поршенька служил ограничитель 5 из
нихромовой проволочки. Установка поршенька в исходное положение
осуществлялась с помощью проволочного штыря 6, прикрепленного к никелевому
цилиндрику 7, который можно было перемещать с помощью наружного магнита.
С помощью осциллографа с памятью (С1-29) измерялось время пролета
поршеньком известного расстояния между ограничителем 5 и сечением трубки,
просвечиваемым узким коллимированным пучком света от лампочки 8. Для
измерения времени пролета развертка осциллографа запускалась одновременно
с началом пропускания через трубку прямоугольного импульса тока
длительностью tc, а на вход осциллографа
подавался сигнал с фотодиода 9, по которому определялось время пролета
поршеньком расстояния, равного длине измерительной базы
Lб.
На последнем моменте остановлюсь более
подробно. Изготовленный коллиматор состоял из лампочки, нить которой
находилась в фокусе линзы, самой линзы, формирующей параллельный пучок
света, и диафрагмы, которая из параллельного пучка света вырезала уже
узкий пучок сечением 0,15×6 мм. Этим узким пучком и просвечивалась
баллистическая трубка. Конструктивно расстояние между плоскостью электрода
трубки, обращенной к разряду, и плоскостью просвечивающего пучка света не
удалось сделать менее 70 мм. Поэтому минимальная длина измерительной базы
в момент пересечения поршеньком пучка света равнялась 60 мм с учетом того,
что длина поршенька составляла 10 мм. Впоследствии я стал определять
скорость поршенька не по базе, а по времени перекрытия поршеньком узкого
пучка света. Но далее продолжим рассмотрение результатов, полученных на
основе варианта с измерительной базой, так как из них можно оценить
влияние трения поршенька о стенки трубки на его скорость.
Время
пролета поршеньком базы длиной 66 мм превышало время существования плазмы
разряда в среднем на два порядка. Это означает, что поршенек в течение
существования плазмы разряда оставался практически неподвижным. Таким
образом, скорость его v после прекращения воздействия на него
плазмы разряда оставалась постоянной и ее можно было рассчитать по
известной длине измерительной базы Lб и измеренному
времени пролета этой базы поршеньком.
Ошибка в определении
величины импульса количества движения, сообщаемого поршеньку, определяется
погрешностью измерения скорости, сообщаемой поршеньку плазмой разряда. В
частности на величину скорости могут оказывать влияние силы трения,
действующие на поршенек. Влияние этих сил будет тем больше, чем больше
длина измерительной базы и масса поршенька. Для выяснения зависимости
измеряемого импульса от массы поршенька и длины измерительной базы были
поставлены контрольные опыты. Результаты одной из серий опытов
представлены на рис. 35.
По оси ординат отложены значения импульса
количества движения, рассчитанные по измеренным скоростям поршенька, в
зависимости от длины базы измерения Lб и массы поршенька
m. Как видно из графиков, величина систематической погрешности
падает с уменьшением массы поршенька и длины измерительной базы. При длине
базы 66 мм усредненные (по четырем измерениям) значения импульсов
количества движения, измеренные с помощью поршеньков массой от 50 до 490
мг, отличаются менее, чем на 4%. Систематическая часть погрешности
уменьшается с укорочением длины измерительной базы. Разброс измеренных
значений величины импульса количества движения при m=const не
превышал 2% от среднего значения при длине базы 66 мм.(см. таблицу ниже)
Форма и материал поршенька на результаты измерения влияния не
оказывали. Чаще всего использовались поршеньки, выточенные в форме,
похожей на обычную деревянную катушку для швейных ниток.
Опытным
путем было выяснено, что воспроизводимость параметров плазмы от разряда к
разряду наступает не сразу, а после проведения в трубке 2-3 разрядов,
причем наибольшее различие наблюдается между первым и вторым разрядом.
Указанная закономерность повторялась после многочасового перерыва в работе
установки или при переходе установки на работу с другим газом. Добиться
устранения разницы между первым и последующим импульсами не удалось ни
путем многочасового прогрева трубки при температуре 100-120°C и вакууме
10-4 тор, ни при длительной обработке с помощью тлеющего
разряда.
Установить число импульсов, после которых наступает
воспроизводимость параметров плазмы, удается не только наблюдая за
интенсивностью спектральных линий с помощью фотоумножителя, но и путем
измерения импульсов от давления, сообщаемого поршеньку плазмой разряда.
Вследствие того, что импульс, получаемый поршеньком, является интегральным
параметром, этот способ является чувствительным ко всяким малым изменениям
в условиях проведения разрядов (даже погодным! - за счет колебаний
температуры и атмосферного давления), которые не удается заметить при
наблюдении за интенсивностью спектральных линий.
Изменение
величины импульса в зависимости от порядкового номера разряда, измеренного
в двух сериях разрядов после длительного перерыва в работе установки,
показано в таблице. Серии разделены промежутком времени около девяти
дней.
| Зависимость импульса количества движения, сообщаемого поршеньку, от порядкового номера разряда* | |||||||
| Номер серии разрядов | Величина импульса количества движения,
гм/сек | ||||||
| Порядковый номер разряда в серии | |||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| Серия 1 | 2,07 | 1,42 | 1,36 | 1,36 | 1,37 | 1,36 | 1,36 |
| Серия 2 | 1,90 | 1,51 | 1,39 | 1,40 | 1,39 | 1,39 | 1,40 |
| * Гелий; трубка ø19×160 мм; начальное давление газа 10 тор; амплитуда прямоугольного импульса тока 11 кА; длительность импульса тока 50 мкс; величина тока предварительно зажигаемого тлеющего разряда 60 ма. | |||||||
Я подробно рассказываю о характере воспроизводимости
параметров разряда по той причине, что это было существенно, так как
различные параметры плазмы разряда измерялись не в одном, а большей
частью в нескольких опытах. И не потому, что это было невозможно сделать
в одном опыте, а просто часто нехватало необходимого количества
аппаратуры. Например, измерить ход давления в разряде пьзодатчиком и
импульс, сообщаемый плазмой поршеньку при баллистическом методе измерения
количества движения, было затруднительно из-за отсутствия второго
осциллографа с памятью. Но при этом пьезодатчик был установлен на
разрядной трубке со стороны заземленного электрода, а баллистическое
устройство на электроде, к которому подводились высоковольтные импульсы,
поэтому получить необходимые данные за один разряд было сложно, так как
нужно было использовать фотосъемку осциллограмм на втором осциллографе.
Поэтому при последовательной регистрации параметров разряда требовалась
стабильная воспроизводимость разрядов, убеждаться в которой приходилось
путем многократных повторов опытов.
Рассмотрим теперь основной
вариант калибровки пьезодатчика с помощью описанного баллистического
способа измерения количества движения P, сообщаемого поршеньку
плазмой импульсного разряда. Величина P=mv равна импульсу силы
sp(t)=sku(t), действующей на поршенек со стороны плазмы, созданной
импульсом тока, и существующей в течение времени tпл:
Интеграл в левой части этого равенства определяется из обработки осциллограммы напряжения u(t) с пьезодатчика, величина скорости v=const измеряется c помощью осциллографа. После этого остается лишь рассчитать величину k. Опыты, проведенные с разрядами при различных токах и давлениях, указали на постоянство величины k в обследованном диапазоне режимов. Согласно этим измерениям величина коэффициента пропорциональности оказалась равной k=15,3 атм/в с точностью ± 8% и практически совпала со значением, полученным при калибровке датчика падающим шариком (15,9 атм/в). Помню, что этот результат, указывающий на практическую эквивалентность динамических способов калибровки датчика как с помощью сосредоточенной, так и распределенной нагрузки, меня совсем не обрадовал, но об этом чуть позже, в следующем разделе.
Заканчивая этот раздел, хочу отметить, что измерить давление в условиях изучаемого разряда можно одним только баллистическим методом, не привлекая для этого пьезодатчик. Действительно, для создания разрядов использовался генератор тока, формирующий через разрядную трубку прямоугольные импульсы тока с малыми фронтами. Хочу напомнить, что слова "генератор тока" означают, что внутреннее сопротивление генератора существенно превышает сопротивление нагрузки, поэтому величина тока от нагрузки зависит слабо. В проводившихся экспериментах внутреннее сопротивление генератора, как минимум, в семь раз превышало сопротивление нагрузки в виде разрядной системы. В этих условиях осциллограммы напряжения на электродах трубки, измеряемые с помощью компенсированного омического делителя, а также интесивности спектральных линий и сплошного спектра, регистрируемых с помощью фотоумножителя, фиксировались на осциллографе с памятью или на обычном осциллографе с помощью фотоаппарата. Из вида этих осциллограмм следовало, что существуют режимы (определяемые током, начальным давлением, родом наполняющего газа, диаметром разрядной трубки, способом инициирования разряда), в которых во время подавляющей части длительности импульса тока упомянутые параметры оставались постоянными. Кроме того, при низких начальных давлениях (< 10 тор) газа в разрядной трубке можно было выбрать длительность импульса тока, которая существенно превышала время распада плазмы. Поэтому для описанных режимов, можно предположить, что и давление ведет себя аналогичным способом, то есть на полке импульса тока оно остается постоянным. Если это так, то импульс силы от давления, действующий на поршенек баллиcтического устройства, можно описать следующим простым выражением: sptc, где, напомню, tc обозначает длительность прямоугольного импульса тока. С другой стороны, импульс силы равен приращению импульса количества движения поршенька за время действия силы, равного в данном случае mv. С учетом сказанного можно сразу записать выражение для давления на полке прямоугольного импульса тока через измеряемые внешние параметры:
Чтобы устранить влияние переходных стадий разряда,
могущих исказить величину истинного значения давления при использовании
метода определения давления, основанного на формуле (5), можно
использовать дифференциальный баллистический метод. Этот метод требует
двух измерений импульса количества движения, получаемых поршеньком
баллистического устройства при различных длительностях прямоугольного
импульса тока, равных, соответственно, tc1 и
tc2, причем для определенности считаем, что
tc1 > tc2.
Идея
дифференциального баллистического метода заключается в том, импульс силы,
действующей на поршенек в течение промежутка времени tc1
- tc2, равен разности измеренных значений количества
движения поршеньков mv(tc1) - mv(tc2). С
учетом этого формула для расчета величины давления на полке импульса тока
в этом случае выглядит, как:
После того, как описанный баллистический метод выполнил
свое основное назначение калибровки пьезодатчика, он из-за своего
интегрального характера, а, следовательно, и своей чувствительности (см.
таблицу выше) к изменениям условий опытов (например, начало меняться
атмосферное давление, а, значит, и плотность газа в разрядной трубке;
изменились параметры исследуемого газа из-за замены газового баллона и т.
д.) стал использоваться для контроля стабильности параметров
разряда.
Баллистическое устройство было оформлено в виде отдельного
мобильного блока, который можно было за несколько минут установить или
снять с фланца разрядной трубки. Мобильность обеспечивалась за счет
быстродействующего зажима, обеспечивающего вакуумно-плотную стыковку
устройства и трубки.
Прежде чем перейти к рассмотрению результатов количественного исследования параметров разрядов, в интерпретации которых измерения давления сыграли решающую роль, обрисуем предварительно общую картину развития канала сильноточных ограниченных стенками разрядов. Это позволит более четко ориентироваться в излагаемом материале.
2. ФЕНОМЕНОЛОГИЧЕСКОЕ ОПИСАНИЕ ПОВЕДЕНИЯ КАНАЛА СИЛЬНОТОЧНЫХ
РАЗРЯДОВ
СФР-грамма представляет собой развертку во времени процесса развития канала в одном из поперечных сечений трубки. Развертка осуществлялась путем перемещения изображения канала в сечении трубки по фотопленке за счет вращающегося зеркала камеры в виде трехгранной пирамиды. Зеркало могло вращаться со скоростью до 90000 об/мин.
В результате экспериментирования в непосредственном личном контакте с токарным и фрезерным станками, которые "на лету" обеспечивали внесение изменений в создаваемые опытные образцы, было установлено, что при разрядах в гелии, азоте, аргоне и воздухе в получившейся конструкции разрядной трубки и найденных способах инициирования разрядов возможно формирование трех разновидностей осесимметричных конфигураций плазмы. Разряды, обеспечивавшие получение этих конфигураций в работе "Формирование симметричных сильноточных разрядов" предложено назвать центральным, пристеночным и промежуточным.
В центральном типе канал разряда зарождается на оси разрядной трубки и затем расширяется к стенкам разрядной трубки. В зависимости от амплитуды тока, начального давления газа в трубке, радиуса трубки образовавшийся канал частично или полностью заполняет сечение трубки. Этот тип разряда формируется в наиболее широком диапазоне давлений, причем его формирование не вызывает особых затруднений. Наиболее простой способ его формирования следующий: необходимо перед пропусканием через разрядную трубку прямоугольного импульса тока зажечь тлеющий разряд. Величина тока тлеющего разряда существенного значения не имеет. В опытах она варьировалась от долей до сотен ма. Тлеющий разряд зажигался за несколько десятых долей секунды до подачи прямоугольного импульса тока. Для решения поставленных задач использовался в основном только этот тип разряда.
В пристеночном типе развитие разряда происходит непосредственно от стенок разрядной трубки. По всей внутренней поверхности трубки возникает светящаяся цилиндрическая область, которая расширяется от стенок разрядной трубки к ее центру. Этот тип возникает, если с помощью короткого (около 1 мкс) высоковольтного поджигающего импульса инициировать в трубке возникновение слаботочного разряда (порядка десятков ма), а затем спустя 40-50 мкс пропустить через трубку прямоугольный импульс тока.
В промежуточном типе канал сильноточного разряда возникает в виде цилиндрической области, которая приблизительно на 15-20% меньше внутреннего диаметра разрядной трубки. Эта плазменная трубка по мере развития разряда утолщается и, в конце концов, может заполнить все сечение кварцевой разрядной трубки. Формирование промежуточного типа происходит так же, как и формирование пристеночного, но только с большей задержкой (примерно 150 мкс) начала пропускания через трубку прямоугольного импульса.
Пристеночный и промежуточный типы разрядов были сформированы в азоте при начальном давлении 1 тор и аргоне при начальных давлениях наполняющего газа 1 и 10 тор. При более высоких давлениях эти разряды сформировать не удалось. В воздухе указанные разряды были сформированы при начальном давлении 1 тор, при более высоком давлении исследования не проводились.
Развитие канала сопровождается возникновением ударной волны, которая отрывается от границы канала и затем, отражаясь от стенок разрядной трубки, многократно проходит через плазму канала разряда в виде светящейся волны, свечение которой хорошо видно на СФР-граммах разрядов.
В указанных трех типах разрядов осесимметричные конфигурации плазмы возникают сразу после подачи прямоугольного импульса тока. В процессе своего развития каналы описанных типы разрядов превращаются в осесимметричные физически идентичные плазменные каналы. Это вытекает из наблюдений за давлением с помощью пьезодатчика и интенсивностью спектральных линий с помощью фотоумножетеля.
Особенно показательны СФР-граммы разрядов в трубках большого диаметра при относительно низких амплитудах прямоугольного импульса тока, приведенные ниже.

- аб - стадия аномального тлеющего разряда,
- бв - стадия быстрого расширения канала,
- вг - стадия медленного расширения,
- гд - участок увеличения свечения плазмы разряда
- де - участок свечения плазмы разряда постоянной интенсивности,
- еж - послесвечение плазмы разряда после обрыва тока.

- аб - стадия аномального тлеющего разряда,
- бв - стадия исчезновения свечения,
- вг - стадия быстрого расширения внутренней границы кольцеобразного канала разряда к центру трубки,
- гд - стадия "рассасывания" центральной холодной области плотного газа,
- де - участок увеличения свечения плазмы разряда,
- еж - участок постоянной интенсивности свечения плазмы,
- жз - послесвечение плазмы после обрыва тока.
В процессе экспериментирования удалось осуществить формирование осесимметричных многокилоамперных электрических разрядов не только в кварцевых трубках, но и в трубках медных, что на первый взгляд представляется абсурдом. Возможность такого формирования была установлена с помощью пьезоэлектрического датчика давления. Датчик регистрировал одинаковый ход давления в разрядах, условия формирования которых отличались лишь материалом разрядной трубки. В одних опытах использовалась привычная кварцевая трубка, в других - непривычная медная. Единственное, что надо было соблюсти, - это обеспечить зазор порядка нескольких миллиметров между торцами медной трубки и медными электродами в используемой конструкции разрядной системы. Кроме того, в медной трубке обязательно следовало зажигать слаботочный тлеющий разряд перед подачей прямоугольного импульса тока. Сформировать сильноточные разряды в медных трубках удавалось при сравнительно низких амплитудах тока (не выше 4 кА) и относительно высоких начальных давлениях газа в трубке >10 тор. Но этот случай детально не исследовался. Тем не менее, можно сказать, что пристеночный слой газа является неплохим изолятором: шунтирования канала разряда не происходило в течение десятков и даже сотен мкс.
В водороде сформировать разряды, в которых плазма
осесимметрична во все моменты их существования большей частью не удается.
На СФР-граммах наблюдается следующая картина: внешняя граница канала
разряда с момента возникновения и до соприкосновения со стенками в
подавляющем числе случаев обладает цилиндрической симметрией, но в самом
канале наблюдаются оптические неоднородности. Масштаб этих неоднородностей
при начальном давлении водорода 1 тор порядка диаметра трубки и исчезают
они приблизительно через 50-100 мкс. С увеличением начального давления
масштаб оптических неоднородностей уменьшается и судя по СФР-граммам, они
быстрее исчезают. Так, при давлении водорода в трубке 10 тор оптические
неоднородности исчезают из канала через 30-45 мкс.
Регистрация хода
интенсивностей спектральных линий при разрядах в водороде с помощью
фотоумножителя показала, что при осевом наблюдении колебания интенсивности
линий малы, а при радиальном сначала наблюдаются значительные их
колебания, которые затем практически пропадают.
Одной из главных задач исследования было получение осесимметричной квазистационарной плазмы. Под этим термином понималась плазма, в которой отсутствовали макроизменения, кроме того, оставались практически постоянными давление, напряженность электрического поля, интенсивность излучения в спектральных линиях и сплошном спектре. Добиться этого удалось лишь для режимов, в которых формирование квазистационарной стадии заканчивалось раньше момента наступления испарения стенок разрядной трубки.
Время существования квазистационарной стадии разряда
ограничивается началом активного испарения стенок разрядной трубки. Причем
при больших амплитудах тока (генератор к концу своего существования
обеспечивал формирование импульсов тока с амплитудой до 150 кА при
напряжении холостого хода 12 кВ) квазистационарная стадия, вообще,
отсутствовала. Испарение стенок могло начаться, например, до того, как
канал разряда успевал расшириться до половины диаметра разрядной трубки.
Так как основной задачей работы было получение чистой
квазистационарной плазмы и исследование ее свойств, то при исследовании
ограничивались режимами, при которых такая стадия успевала возникнуть до
наступления испарения стенок трубки.
СФР-грамма типичного режима
приведена ниже.

На фотографии изображена СФР-грамма разряда в азоте с
испарением стенок разрядной трубки: А- начало испарения. Трубка размером ø
30× 160 мм, начальное давление азота в трубке 10 тор, ток предварительно
зажигаемого тлеющего разряда 30 ма, амплитуда прямоугольного импульса тока
40 кА. От начала развития канала тока до начала испарения прошло 22 мкс.
Начало наступления квазистационарного режима, помимо СФР-грамм,
уточнялось по осциллограммам хода интенсивности спектральных линий,
которые регистрировались фотоумножителем, по осциллограммам напряжения и
давления. Примеры осциллограмм хода интенсивности спектральных линий
представлены на снимках для гелия и
азота.
Причем при разрядах в водороде,
в начальной стадии которых возникают неоднородности, наступление
квазистационарной стадии дополнительно уточнялось наблюдениями за ходом
излучения спектральных линий в радиальном направлении.
Установить
момент наступления испарения стенок можно разными способами: по отснятым
СФР-граммам, осциллограммам напряжения
на электродах трубки, осциллограммам спектральных
линий, осциллограмме сигнала с пьезодатчика и, наконец, с помощью
измерения импульса количества движения поршенька баллистического
устройства. Съемка СФР-грамм хороша на стадии предварительном ознакомлении
с режимом разряда, но не оперативна. Осциллографирование интенсивности
спектральных линий тоже кропотливое занятие, так как не все линии начинают
реагировать одновременно на наступление испарения. Наиболее оперативный
способ - осциллографирование напряжения на электродах трубки, но по ним
бывает затруднительно определить точно момент наступления испарения.
Баллистический метод позволяет, во-первых, "нащупать" момент
существенного испарения стенок следующим образом: проводится серия
разрядов, отличающихся тем, что каждый последующий разряд проводится с
увеличенной длительностью импульса тока. Увеличивая длительность каждого
последующего импульса на одно и то же значение, например, 3 мкс, можно
определить на каждой стадии величину приращения импульса количества
движения поршенька. Если давление выходит на стационарное значение, то
приращения будут практически одинаковыми. Небольшое уменьшение их будет
происходить при значительных амплитудах тока за счет спада последней из-за
разрядки силовой батареи конденсаторов генератора. Увеличение приращений
импульса количества движения укажет на возникновение испарения,
нарушающего чистоту плазмы. Следует отметить, что по сравнению с
СФР-граммами баллистика запаздывает с определением наступления момента
испарения, но она фиксирует начало интенсивного испарения. Кроме того,
баллистика позволяет контролировать идентичность распадов, что важно при
проведении серии опытов, например, при исследовании распада плазмы с
использованием фотографической регистрации спектров с помощью
спектрохронографа.
Спектрохронограф при съемке спектров на пленку
обепечивал открытие щели спектрографа на 4 мкс в любой заранее выбранной
стадии существования плазмы разряда, причем момент открытия не только
задавался настройкой схем задержки, но и контролировался по осциллографу с
памятью. Для этого импульс с токоизмерительного шунта и импульс с
фотоумножителя, контролировавшего открытие щели спектрографа путем
регистрации возникавшей в корпусе спектрографа паразитной засветки, через
схему сложения сигналов подавались на осциллограф с памятью. При этом на
экране осциллографа можно было видеть изображение положительного токового
импульса и наложенного на него отрицательного импульса засветки и тем
самым контролировать, что экспозиция фотопленки произошла именно в
заданный момент. На зарисовке
реальной осциллограмы показан случай, когда съемка спектра произошла
уже после обрыва токового импульса, то есть при распаде
плазмы.
После этих предварительных замечаний, важных для
последующего понимания, рассмотрим некоторые результаты и выводы,
полученные при совместном анализе результатов измерения давления с помощью
изложенных выше методов, и результатов спектроскопического измерения
интенсивностей излучения плазмы в спектральных линиях и сплошном спектре,
добытых с помощью спектрохронографа.
3. ИССЛЕДОВАНИЕ ВОДОРОДНОЙ ПЛАЗМЫ
3. 1. Задачи, подлежащие решению.
После того, как установка полностью "притерлась" и был
пройден этап предварительных отладочных опытов и доработок, отснять на
пленку спектры плазмы разряда, как в стационарной стадии, так и при
распаде, уже не представляло труда. Так, съемка спектров для выбранных
условий разряда (ток, давление, род газа, диаметр трубки) занимала по
времени около четырех часов работы установки. Причем снятые спектры
дополнялись осциллограммами давления и снимками спектра эталонного
источника абсолютно черного тела с температурой 39000K для определения
абсолютных спектральных интенсивностей. Для повышения надежности добываемых
результатов серии опытов повторялись многократно и обрабатывались
независимо. Возможные систематические ошибки, могущие возникнуть при
обработке спектрограмм, выявлялись во время контрольной обработки отдельных
спектрограмм третьим лицом. Были получены спектрограммы разрядов в
водороде, гелии, азоте и аргоне.
Типичные спектрограммы, снятые при
изучении распада водородной и гелиевой плазм, представлены на фотографии,
на которой зафиксированы спектры разрядов в водороде и гелии, относящиеся
к различным фазам существования плазмы разряда. Водород: а -
квазистационарная стадия, б и в – через 32 и 60 мкс после
обрыва тока. Гелий: г – квазистационарная стадия, д – через
52 мкс после обрыва тока.
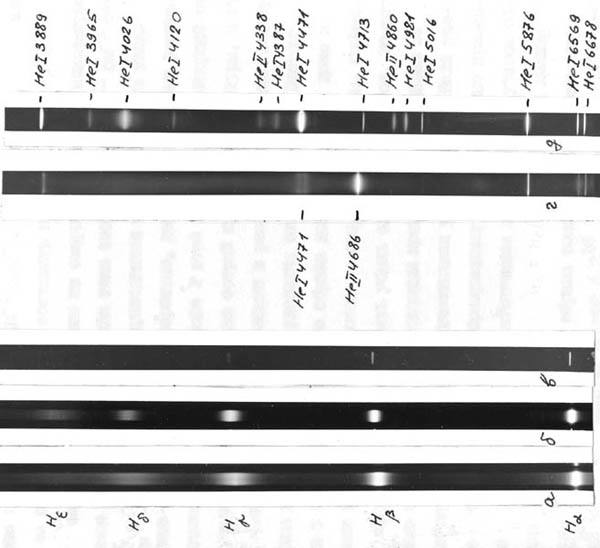
Результаты обработки некоторых из полученных спектрограмм были опубликованы. Но, прежде чем обсуждать эти результаты, обрисуем задачи, которые мне, как аспиранту, следовало решить и те теоретические предпосылки, которые предполагалось использовать для интерпретации данных, которые должны были быть получены в результате выполнения аспирантской работы на соискание ученой степени к.ф.м.н..
Как рассказано в "Истории исследования", задачи, которые следовало решить при подготовке кандидатской работы, были следующими:
- Разработать и собрать установку для создания плазмы с температурой
5-7 эв при давлении порядка атмосферного или выше, причем первоначально
было не ясно, какими параметрами должно обладать устройство, способное
создавать такую плазму. Предположительно таким устройством мог быть
генератор, собранный на тиратронах или игнитронах. Причем предполагалось
исследовать плазму только одного газа - то ли аргона, то ли азота, уже
точно не помню,
- Собрать, что-то вроде скоростного затвора, позволяющего снимать
спектры плазмы разряда в любой момент ее существования с достаточно
хорошим временным разрешением. Имелись образцы такого затвора,
состоящего из шторки в виде текстолитовой пластиночки со щелью и
проволочной петли из нихрома, к которой шторка в исходном состоянии была
плотно прижата своим торцом. Шторка проскакивала мимо щели спектрографа,
когда через нихромовую петлю пропускался импульс тока.
- Снять чистовые спектры распада плазмы на спектрографах ИСП-51 с
камерой F=270 мм и ИСП-28 и провести стандартную обработку полученных
спектрограмм. Причем абсолютизирование спектров предполагалось
осуществить сначала с помощью обычной вольфрамовой ленточной лампы.
- На основе результатов обработки спектрограмм определить коэффициенты рекомбинации плазмы, ради получения которых и открывалась эта кандидатская работа. Причем на основе существующих теоретических критериев считали, что в исследуемых плазмах будет реализоваться частичное ЛТР, так как ожидаемые в опытах концентрации электронов существенно превышали значения, требуемые для реализации чЛТР.
- С самого начала работы наибольшее внимание уделялось разработке
генератора импульсов тока большой амплитуды. Этой частью работы я
занимался с большим энтузиазмом, так как это была моя "стихия": до этого
не раз приходилось собирать самые разнообразные генераторы в течение более 10 лет.
Первоначально был собран тиратронный генератор периодических импульсов,
генерирующий прямоугольные импульсы тока амплитудой (максимум) до 400 А
и частотой 5 гц. Этот генератор не обеспечил получение плазмы с
запланированными параметрами, но показал, что спектр разряда можно снять
всего за один импульс. Поэтому разработку этой схемы оставил, но получил
на нее авторское свидетельство - в отделе аспирантуры говорили, что
неплохо бы украсить будущую диссертацию, помимо печатных статей, если не
документом о внедрении результатов работы в "народное хозяйство", то
хотя бы авторским свидетельством на изобретение. Вот такое "украшение" и
оформил. После этого перешел на схему генератора,
формирующего лишь одиночные импульсы, которая явилась основной.
Использование мощных водородных тиратронов позволило сформировать с ее
помощью импульсы тока амплитудой до 2 кА и длительностью до 600 мкс. В
этом режиме тиратроны "выдерживали" около 10-15 импульсов, после чего
их следовало заменять. Но, самое главное, запланированные параметры
плазмы не достигались.
Встал вопрос о замене тиратронов более мощными устройствами. Я склонялся к воздушным разрядникам или разрядникам высокого давления, с которыми имел определенный опыт работы, как в изготовлении, так и эксплуатации. Однако мой руководитель предложил, как мне сейчас представляется, более оптимальное решение. Он устроил мне "экскурсию" в институт атомной энергии им. И. В. Курчатова, где я воочию увидел вакуумные дисковые разрядники, кроме того, там нам дали ссылки на журналы ЖТФ за 1966-1968 г., в которых было опубликовано их описание. Недели примерно через три или четыре после этой экскурсии мне удалось в своей домашней мастерской "слепить" два вакуумных разрядника диаметром 150 мм. Замена ими тиратронов сразу позволила поднять амплитуду тока до 6-8 кА. Этого также оказалось не достаточно, кроме того разрядники плохо выдерживали формирование импульсов тока длительностью в 600 мкс. Их приходилось часто чистить. Поэтому было принято решение перейти на разрядники диаметром около 500 мм. В итоге после кропотливой длительной работы был собран генератор прямоугольных импульсов тока, способный к концу аспирантского срока формировать одиночные импульсы с амплитудой до 40 кА c крутым задним фронтом при напряжении холостого хода 5 кВ.
Значительная часть времени при доводке генератора уделялась получению прямоугольных импульсов тока с крутыми фронтами. Это осуществлялось, во-первых, за счет усложнения монтажа силового контура с целью уменьшения его индуктивности. Монтажная схема силового контура по состоянию на время окончания аспирантyры представлена на рисунке. Во-вторых, (уже, в основном, после защиты диссертации) за счет увеличения рабочего напряжения конденсаторной батареи генератора. Так, переход с 5 кВ на 12 кВ позволил формировать прямоугольные импульсы тока со следующими параметрами (при работе генератора в режиме короткого замыкания): амплитуда импульса - 60 кА, время нарастания переднего фронта импульса - 8 мкс, время спада заднего фронта импульса - 4 мкс, длительность импульса при 10% спаде амплитуды на полке импульса - 50 мкс.
Хочу упомянуть один полезный инструмент, без которого не удалось бы выполнить эту работу так, как хотелось. Это небольшой расточной патрон, пригодный, в частности, для работы с моими станочками, который был "слеплен" практически на "на коленках". С помощью этого патрона было сделано большинство отверстий, расточено пазов, отфрезеровано поверхностей почти во всех деталях (разрядники, разрядная система, спектрохронограф, электролизер, источник эталонного излучения, корпуса фотоприставок, детали генераторов импульсов и т. д.) экспериментальной установки. Использование его на порядки сократило время на выполнение механических операций, нужда в совершении которых была постоянна, и которые, зачастую, приходилось выполнять в большом количестве. Без патрона с этим было бы просто не справиться.
- Отработана и изготовлена конструкция разрядной трубки, обеспечившая
создание плазменных конфигураций с запланированными параметрами,
пригодных для точных спектроскопических исследований, то есть обладающих
цилиндрической симметрией. В этом случае, как уже упоминалось, можно
получить информацию о распределении интенсивностей излучения плазмы по
радиусу разряда, применяя преобразование Абеля к снимкам спектров,
отснятым в радиальном направлении.
- Вместо вольфрамовой лампы, интенсивность излучения которой была на много
порядков меньше интенсивности излучения полученной плазмы, в качестве
эталона абсолютно черного тела с температурой 39000К был использован
капиллярный разряд, возникавший при пропускании через отверстие ø2 мм в
текстолитовой пластинке толщиной 10 мм прямоугольного импульса тока с
амплитудой в 9 кА . Этот капиллярный источник запитывался от собранного
генератора прямоугольных импульсов тока, поэтому сама конструкция
эталонного источника получилась компактной, очень простой, а, главное,
посильной для моего фрезерного станочка. Внешний вид его изображен на
фотографиях установки под номером 4 и
разрядной трубки под номером 7.
- Для съемки спектров плазмы разряда в выбранные моменты ее
существования относительно начала разряда первоначально предполагалось
использовать управляемый затвор вместе со спектрографом. Затвор
представлял собой подвижную шторку с прорезью. Шторка проскакивала перед
входной щелью спектрографа в результате воздействия на нее теплового
расширения проволочки, через которую в определенный момент разряжался
конденсатор. Изготовил несколько вариантов таких затворов вместе с
электронной схемой управления. Наименьшее время экспозиции, которое
удалось получить с их помощью, составило 15 мкс. Для исследования распада
плазмы это было многовато. Поэтому от дальнейших попыток
усовершенствовать это устройство отказался.
Для съемки спектров плазмы разряда с разрешением 4 мкс в любом заранее выбранном моменте ее существования с точностью ±0,5 мкс разработал и изготовил управляющий спектрохронограф, изображенный на снимке разрядной трубки под номером 6. Основу его составлял дюралевый диск с радиальной щелью, вращающийся со скоростью 7500±3 об/мин, устанавливаемый параллельно входной щели спектрографа на расстоянии 0,6 мм от нее. Щель вращающегося диска периодически открывала щель спектрографа. За 150 мкс до открытия входной щели спектрографа вырабатывался сигнал синхронизации, который запускал процесс формирования разряда в трубке через схему задержки. В качестве схемы задержки использовался генератор Г5-15. Величины времени задержки импульса синхронизации выбиралась так, что к моменту открытия щели спектрографа плазма находилась в той фазе своего существования, спектр излучения которой было запланировано сфотографировать.
Питание спектрохронографа и контроль числа оборотов диска осуществлялись с пульта управления скоростной фотокамеры СФР-1, имеющего встроенный кварцевый частотомер, поэтому спектрохронограф получился компактным и не сложным для изготовления. Электродвигатель для него приобрел на московском птичьем рынке. Для изготовления спектрохронографа понадобилась дюралевая заготовка размером около ø25×250 мм, которую нигде не мог сразу достать. Поэтому из куска графита, нихрома и шамотных пластинок собрал небольшую плавильную печку сопротивления, которой можно было манипулировать на весу одной рукой. С ее помощью из дюралевой стружки выплавил и отлил нужную заготовку. Эта печка потом неоднократно выручала, экономя массу времени. Так, с ее помощью был отлит штурвал, кажется, из бронзовой стружки (на общем виде помечен номером 18) механизма заземления конденсаторной батареи емкостью 2400 мкф, заряжаемой до 5, а впоследствии после ее модернизации и до 12 кВ.
- Исследование плазмы сильноточного разряда, хотелось начать с опытов,
в которых разрядная трубка была бы заполнена водородом, как наиболее
простым по своей структуре газом. Однако это долго не удавалось делать,
так как в соответствии с правилами техники безопасности держать баллон с
водородом, в отличие от других газов, в лаборатории было нельзя. Поэтому
собрал небольшой электролизер прямо в установке, ведь, водорода
требовалось крайне мало. С целью получения водорода без вредных примесей
электролизер был специальной конструкции, исключавшей возможность
загрязнения водорода кислородом. Первоначально опробованный небольшой
аппарат Киппа, как показали спектрограммы разряда, не очень подходил в
качестве генератора водорода.
Получаемый от электролизера водород пропускался через колонку c осушителем и змеевик, погруженный в жидкий азот.
- Для измерения давления в разрядной трубке был изготовлен
пьезодатчик, калибровка его была выполнена с помощью падающего шарика.
Об этом подробно рассказано в самом начале этой страницы.
- Анализ данных, полученных при решении третьей задачи, показал, что предположение о чЛТР, которое согласно известным критериям должно "железно" реализоваться в полученных плазмах, не работает. Поэтому использовать эти данные для решения четвертой задачи стало проблематично, поэтому я переформулировал первоначальную цель диссертации, которую доработал и защитил уже без руководителя (см. "История исследования...").
3. 2. Затруднения, связанные с применением спектроскопических методов.
Чтобы наглядно выявить суть возникших затруднений,
постараюсь сначала, насколько это мне удастся, обрисовать те
представления, на которых базируется модель чЛТР.
В лабораторных
плазмах малого размера по сравнению с величиной пробега излучения, выход
излучения является нескомпенсированным процессом, приводящим к отклонению
заселенностей возбужденных состояний атомов и ионов в плазме от
равновесного состояния, которое существует в однородной безграничной
плазме. В такой безграничной плазме каждый акт испускания излучения
компенсируется обратным актом - поглощения излучения. Состояние такой
плазмы можно описать заданием химического состава плазмы и двух внешних
параметров, например, давления и температуры. Если это известно, то все
остальные параметры такой плазмы рассчитываются на основе известных
термодинамических отношений. Однако это идеализированный случай полностью
равновесной плазмы.
Внутренние параметры реальной плазмы могут
существенно отличаться от равновесных параметров, несмотря на совпадение
химического состава, давления и температуры электронов. Я упоминаю
температуру электронов по той причине, что если в равновесной плазме все
компоненты плазмы описываются единой температурой, то в неравновесной
плазме понятия единой температуры нет, и приходится вводить целый ряд
"температур", характеризующих отклонение того или иного компонента плазмы
от равновесия. Однако, если концентрация электронов в плазме велика, то
влияние выноса излучения на заселенность возбужденных уровней атомов и
ионов уменьшается за счет того, что возрастает доля ударного возбуждения
уровней, которая начинает компенсировать влияние выноса
излучения. Причем с ростом концентрации электронов влияние выноса
излучения продолжает уменьшаться. И может возникнуть такая ситуация, когда
заселенность всех атомных уровней, включая основное невозбужденное
состояние, станет такой, как в случае равновесной плазмы. При этом такая
плазма характеризуется единой температурой, однако, описать интенсивность
излучения данной плазмы термодинамическим выражением нельзя. В этом случае
говорят, что плазма находится в состоянии полного локального
термодинамического равновесия (ЛТР).
Однако состояние полного ЛТР
достижимо в крайне редких случаях - при очень больших концентрациях
электронов. Гораздо чаще встречаются случаи частичного ЛТР, когда
некоторая часть верхних возбужденных уровней описывается равновесными
соотношениями, а остальные ниже лежащие нет. Причем, чем ниже расположен
уровень по энергетической шкале, тем сильнее его заселенность отклоняется
от равновесной.
Чтобы характеризовать степень отклонения
заселенности уровня от равновесного значения используют величину
температуры TeC, рассчитанную по частной
формуле Саха. В случае ЛТР плазмы частная формула Саха связывает величину
заселенности конкретного уровня атома (иона) с величиной концентрации
электронов в плазме и их температурой. Структура этой формулы известна,
она несложная. Такую формулу можно записать для каждого энергетического
уровня. Если измерить концентрацию электронов и абсолютную заселенность
конкретного уровня (то есть количество атомов, находящихся на этом уровне,
в единице объема) в изучаемой плазме, а затем на основе измеренных величин
рассчитать температуру по частной для данного уровня формуле Саха, то
получим значение температуры TeC. Такие
температуры Саха можно определить для целого ряда уровней. Если
заселенность этих уровней описывается моделью чЛТР, то все температуры
Саха должны совпасть с температурой электронов плазмы. Те уровни, для
которых температуры Саха отличны от температуры электронов, уже не
находятся в состоянии чЛТР.
Из теоретических соображений
сформулированы критерии, позволяющие определить, какова должна быть
концентрация электронов в плазме конкретного химического состава, чтобы
все верхние уровни, энергетически расположенные выше выбранного, не
отклонялись от равновесных значений. С учетом этого предложен ряд способов
определения температуры по измеренным спектральным интенсивностям, которые
можно использовать в случае, если установлено, что концентрация электронов
в плазме удовлетворяет сформулированным критериям.
Рассмотрим
зависимости, рассчитанные специально для определения температуры в
водородной плазме по отношению интенсивности водородных линий
Бальмеровской серии к интенсивности сплошного спектра под линией,
предложенные в монографии Грима [2]. Перевод этой монографии появился у
нас в 1969 г., а описанная здесь установка смогла работать практически в
полную силу уже в начале 1971 г..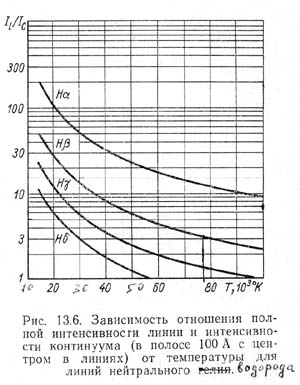 Поэтому появление этой
монографии было весьма кстати. Полученные зависимости представлены на
рисунке. Согласно расчетам автора монографии, при плотности электронов
ne≥ 1014 , см-3, экспериментальная
точность в отношении интенсивностей в 10% приводит в области температур
100000K к ошибке примерно такой же величины. При более низких температурах
ошибки будут значительно меньше до тех пор, пока континуум иона
H- не начнет конкурировать с обычным континуумом, но вклад
континуума отрицательного иона H- существенен лишь при
температурах ≤ 1,3· 104 K.
Поэтому появление этой
монографии было весьма кстати. Полученные зависимости представлены на
рисунке. Согласно расчетам автора монографии, при плотности электронов
ne≥ 1014 , см-3, экспериментальная
точность в отношении интенсивностей в 10% приводит в области температур
100000K к ошибке примерно такой же величины. При более низких температурах
ошибки будут значительно меньше до тех пор, пока континуум иона
H- не начнет конкурировать с обычным континуумом, но вклад
континуума отрицательного иона H- существенен лишь при
температурах ≤ 1,3· 104 K.
Погрешность
теоретических расчетов, используемых для измерения концентрации электронов
по уширению водородных линий, оценена Гримом [2] в 5% для линии
Hβ и около 15% для остальных водородных и водородоподобных
(например, линии HeII4686) линий.
Опубликованные результаты
проведенной работы, касающиеся квазистационарной
стадии разрядов в водороде, сформированных в трубке ø20×205 мм,
воспроизведены в таблице 1 в сокращенном виде. Чтобы уменьшить ширину
таблицы из нее убраны столбцы, в которых приведены единичные оценки
температуры плазмы по электропроводности разряда, скорости звука в плазме,
определению температуры по насыщенной водородной линии Hα.
|
Таблица 1. | |||||||||
| Опыт № |
I, кА | pн, мм рт. ст. |
pпл, атм |
ne, см-3 | Tелк × 10-3, K |
TeC × 10-3, K |
Tоц × 10-3, K |
Tp × 10-3, K | |
| по Hβ | по спл. спектру |
по Hβ | |||||||
| 1 | 3,64 | 1 | 0,35 | 1,74·1016 | 13,8 | > 18,8 | 71 | ||
| 2 | 10,3 | 1 | 1,17 | 5,37·1016 | 1,08·1017 | 46 | 16,8 | > 67 | 77 |
| 3 | 3,72 | 10 | 0,8 | 6,9·1016 | 1,29·1017 | 43 | 8,1 | > 4,6 | 41 |
| 4 | 10,3 | 10 | 2,52 | 1,37·1017 | 3,22·1017 | 40 | 14,2 | > 14,4 | 65 |
| 5 | 13,5 | 10 | 3,35 | 1,86·1017 | 2,6·1017 | 49 | 23 | > 19 | 64 |
| 6 | 11,9 | 30 | 7,0 | 6,3·1017 | 5,1·1017 | 35 | 30 | > 13,3 | 39,5 |
| 7 | 13,5 | 30 | 8,5 | 9,5·1017 | 1,14·1018 | 47 | 39 | > 16,1 | 31,6 |
| Обозначения: I - амплитуда прямоугольного импульса тока; pн-начальное давление водорода в трубке; pпл - давление в плазме разряда; ne - концентрация электронов; Te лк - значения температуры, найденные из отношения интенсивности линии к континууму; Te C - значения температуры, рассчитанные по формуле Саха; Tоц - оценка температуры по давлению pпл и усредненной по объему трубки концентрации частиц; Tp - значения температуры, рассчитанные из давления и концентрации электронов, определенной по уширению Hβ. | |||||||||
Выбор опытов для размещения в таблице осуществлялся по двум правилам. Во-первых, здесь проиллюстрировано, как изменяются параметры плазмы в разрядах при одном и том же начальном давлении с ростом тока. Это цепочки опытов: 1+2; 3+4+5 и 6+7. Во-вторых, показано, как меняются параметры плазмы при одном и том же токе с ростом давления. Это цепочки: 1+3; 2+4+6 (последний с некоторым натягом) и 5+7.
Проанализируем приведенные данные, считая, что калибровка
датчика давления произведена в относительных единицах, а мы хотим
откалибровать его в абсолютных. Для этого нужно отобрать
спектроскопические данные, которые соответствуют модели чЛТР. Однако, если
мы сравним измеренные значения температуры Tлк со
значениями TeС, рассчитанными по измеренным
заселенностям верхнего уровня линии Hβ, то увидим, что
наиболее близки к этой модели только режимы опытов 6 и 7 с очень высокой
концентрацией электронов. Хотя, согласно Гриму, чЛТР в водородной плазме
должно реализоваться, когда концентрация электронов в плазме превышает
ne ≥ 1014, см -3. В проведенных же
опытах достигнуты концентрации электронов, которые на два - три порядка
превышают это значение. Поэтому приведенные графики для определения
температуры электронов по отношению интенсивности линии к континууму
вызвали недоверие. Полученные результаты только качественно согласуются с
представлениями модели чЛТР. Например, видно, как с ростом концентрации
электронов (опыты 3+4+5) температура по Саха сближается с температурой
Tлк, но такая картина должна происходить при
концентрациях электронов на два порядка меньше.
Возвращаясь к опытам 6
и 7, можно предположить, что концентрация нейтралов на этих режимах мала
по сравнению с концентрацией электронов, поэтому давление определяется
только концентрацией заряженных частиц. Из-за большой концентрации
заряженных частиц плазму можно считать изотермичной, это значит что
поступательные температуры электронов и тяжелых частиц практически
совпадают. Если прикинуть теперь величину давления в плазмах опытов 6 и 7
по формуле p=2kTлкne, то получим,
соответственно, 6, 2 и 12, 6 атм. Отношение этих величин равно 2, 03, а
отношение относительных значений давления, измеренных пьезодатчиком равно
1, 2. Стало ясным, что с помощью спектроскопических данных точно
откалибровать пьезодатчик не удастся. Поэтому пришлось заняться решением
задачи калибровки пьзодатчика, приведшую к разработке баллистического
способа калибровки, но который мог и сам по себе измерять давление в
исследуемых условиях. Этот способ подробно описан ранее.
После
того как стало ясно, что калибровка пьезодатчика шариком годится и для
измерения величины распределенной нагрузки, создаваемой давлением плазмы,
продолжим анализ данных таблицы.
Так как измерение температуры плазмы
(температуры электронов) по отношению интенсивности линии к континууму не
вызывало доверия, то была проверена работоспособность этого метода на
режиме, в котором температуру плазмы можно было оценить с хорошей
точностью, не прибегая к спектроскопическим методам.
Такой "глаза
раскрывающий" режим находится в таблице под номером 2. Начальное давление
водорода в разрядной трубке, которую в условиях опытов можно считать
полностью замкнутой, равно 1 мм рт. ст., а температура газа 293 К. При
прохождении через трубку прямоугольного импульса тока стационарное
давление на полке импульса становится равным 1, 17 атм или увеличивается в
760 × 1, 17=890 раз. Но если давление выросло, то и температура газа должна
вырости во столько же раз и стать равной 293×890=260000К. Но при такой
температуре ни молекулы водорода, ни атомы существовать не могут, а есть
только электроны и протоны, так как ион водорода - частица бесструктурная
(протон). При температуре 293К концентрация молекул водорода в трубке
составляет 3,3×1016 см-3. При развале молекул на
электроны и протоны число электронов станет равным 6,6×1016
см-3. Если предположить, что плазма однородна по сечению, это
только занизит оценку величины температуры в центральной зоне и несколько
завысит концентрацию электронов в ней, то с учетом того, что каждая
молекула водорода развалится на четыре частицы температура электронов при
анализируемом режиме будет не ниже, чем 260000/4=65000 K, а концентрация
электронов не выше чем 6,6×1016 см-3. Сравнение
оценочных значений с полученными спектроскопически показывает. Во-первых,
разумное согласие оценочного и измеренного значений концентраций
электронов, определенного по уширению водородной линии Hβ и
расхождение с измеренным по абсолютной интенсивности сплошного спектра.
Последнее превышает завышенное оценочное значение, поэтому заведомо не
верно. Следует отметить, что определение концентрации по уширению
водородных линий слабо зависит от чЛТР, поэтому надежно. Во-вторых, видно,
что метод измерения температуры по отношению интенсивности линии к
сплошному спектру дает сильно заниженное значение. Корректировка
оценочного значения температуры по измеренной концентрации электронов и
давлению приводит к значению температуры электронов в центральной зоне
разряда, равному 77000К, что в 1,67 раза больше измеренного
спектроскопического. Напомню еще раз, что заявленная точность метода 10%,
если концентрация электронов в плазме превышает величину 1014,
см-3. Таким образом, видно, как можно ошибаться, применяя
спектроскопические методы, не проверив предварительно возможность их
использования.
В связи со сказанным выше, хочу добавить, что в сформированных разрядах при низком начальном давлении водорода (0,1 мм рт. ст.), наполняющего трубку, оценка параметров водородной плазмы по измеренному давлению указывает на возможность достижения в трубке ø 20 мм температур не ниже, чем 150000K, при концентрации заряженных частиц не выше, чем 6,6×1015, см-3.
Из-за отсутствия уверенности в реализации чЛТР в
водородной плазме, температура электронов при ее распаде оценивалась
только из давления и концентрации электронов, измеренной по уширению
водородной линий. Однако это оценка температуры сверху, поскольку из-за
рекомбинации электронов и протонов нельзя не учитывать возрастающую
концентрацию нейтральных атомов, но как установить, когда она становится
существенной, опираясь только на величину давления и концентрацию
электронов при распаде, не ясно. Интерпретация осложняется и тем, что при
распаде возможен подогрев плазмы за счет перехода энергии ионизации в
поступательные ее формы, но это только предположение.
Первоначально
планировалось, что измерение температуры электронов по отношению
интенсивности линии к сплошному спектру и давления пьзодатчиком позволит
определить полную концентрацию частиц в любой момент распада плазмы. Если
при этом из найденной полной концентрации вычесть удвоенное значение
концентрации электронов, то получим в чистом виде полную концентрацию
атомов в плазме. Но обнаруженная неработоспособность чЛТР методов в
исследуемых режимах не позволила сделать это.
Отмечу, что и в других
газах при низком начальном давлении газа формируются разряды, в которых
можно получить высокие значения температуры в центральной зоне с
гарантированной оценкой "не ниже чем", ориентируясь на которые можно
оценить реальную точность метода чЛТР. Например, при начальном давлении 1
мм рт. ст., амплитуде тока прямоугольного импульса 15 кА и диаметре трубки
20 мм измеренное
давление в трубке при разрядах в гелии и азоте будет соответственно
1, 02 и 1, 70 атм. Предполагая однородность плазмы в этих случаях и то, что
гелий и азот полностью двукратно ионизованы, найдем, что минимальные
значения температуры электронов в этих разрядах будут не менее 76000 K и
63000 K, соответственно.
В 1971 г. в Москве (МГУ) проходила III Всесоюзная конференция по физике низкотемпературной плазмы, стать официальными участниками ее нам не удалось, но доклад сделать нам дали. Однако, доклад прошел не совсем удачно, так как перед его началом в соседней аудитории начал свое выступление профессор Г. Меккер (кажется, ФРГ), который рассказал о каналовой дуге с температурой плазмы в 25000К. Практически все участники конференции пошли слушать Меккера, поэтому мое сообщение о сильноточном разряде, с помощью которого удалось создать квазистационарную плазму с температурой в 70000К, выслушали только члены президиума конференции, которые не могли пойти на доклад Г. Меккера, и несколько оставшихся участников конференции.
Отклонения от чЛТР обнаружены, помимо, водорода, в гелии азоте и аргоне. Основываясь на схожести результатов можно предположить, что причиной нарушения чЛТР могут быть процессы диффузии в пространственно ограниченных сильноточных разрядах, которые не учитывались при выводе критериев применимости модели чЛТР.
Помню, когда меня волновал вопрос о чЛТР в плазме водорода, из ФИАН'а сообщили, что у них на семинаре будет выступать Г. Грим (США). Можно приехать и задать ему вопросы, будет переводчик. Но попасть на семинар, к сожалению, не смог, в день семинара трамвайные пути завалило снегом.
Таким образом, развитая методика измерения давления привела, с моей точки зрения, к "краху" надежд, изначально возлагаемых на чЛТР методы диагностики, которые в существующем состоянии, не позволили решить поставленную перед кандидатской работой задачу получения надежных сведений о параметрах распадающейся плазмы, созданной газовым разрядом. Но, как говорится, отрицательный результат - это тоже результат и, возможно, даже более важный, чем положительный. Поэтому, в свое время, и решил на нем защищать свою кандидатскую диссертацию. Но жизнь показала (см. "Историю исследования..."), что к отрицательному результату и отношение отрицательное, даже, если он в чем-то и положительный:).
4. ОСНОВНЫЕ РЕЗУЛЬТАТЫ МЕТОДИКИ ИЗМЕРЕНИЯ ДАВЛЕНИЯ
В отличие от сложных спектроскопических методов измерения
давления, требующих уверенности в реализации в плазме хотя бы чЛТР,
прямое измерение давления идейно существенно проще, поэтому с помощью
пьезодатчика не представляло труда обследовать поведение давления в
широком диапазоне режимов сильноточных разрядов. Предел обследованию
ставили лишь время и физические возможности экспериментатора.
Анализ
замеров давления в различных газах, выполненных при разных начальных
условиях, выявил некоторые общие закономерности, о которых уже было
рассказано на предыдущих страницах сайта. Однако, повторяясь, хочу
нарисовать общую картину более компактно и выпукло.
4.1. Основополагающая роль поляризации плазмы в электрическом разряде.
Выяснение этой роли было тесно связано с изучением
поведения давления в электрическом разряде. Поэтому этот раздел насыщен
экспериментальными данными с целью подтверждения выводов, вытекающих из
анализа роли поляризационных плазменных процессов в
плазме.
Результаты измерения давления при наполнении разрядных
трубок различными газами показали, что величины давления не сильно между
собой различаются, и что эти результаты можно приближенно описать
следующей эмпирической формулой, связывающей величину давления p в
трубке с величинами тока I, начального давления и рода газа
po, наполняющего трубку, и радиусом трубки R:
Размерность величин, входящих в эту формулу, дана в системе МКСА (Па, А, м). Расхождение между измеренными значениями давления и рассчитанными по формуле (7) редко превышало 60%.
Поэтому, приближенно, идеализируя ситуацию, можно
полагать, что давление не зависит от рода газа, или, что то же, давление в
разряде не зависит от атомного номера плазмообразующего газа. Возникает
вопрос, а почему это так. Ведь излучательные способности различных газов
могут различаться между собой почти на порядок, то же самое можно сказать
и о их коэффициентах теплопроводности, а вот величины давления в разрядах
разнятся не так сильно, чаще всего, не более, чем в 1,5-2 раза. Попытки
объяснить этот результат привели к выводу, что существенную роль в
разрядах играют поляризационные плазменные процессы, которые вызывают
снижение энергии частиц в плазме по сравнению с энергией тех же частиц, но
находящихся в нейтральном газе. У заряженных частиц (электроны, ионы)
происходит снижение их кулоновской энергии, а у атомов и ионов снижение
энергии ионизации. Подчеркну, что у ионов, как заряженных частиц,
происходит как снижение энергии ионизации, так и снижение кулоновской
энергии. И что важно подчеркнуть, все названные снижения энергии частиц
представляют собой потенциальные формы энергии, - факт, который будет
обсужден ниже.
Установить роль поляризационных процессов удалось не
сразу, хотя давно известно, что, например, в плазме происходит снижение
энергии ионизации находящихся в ней атомов. Причем, если смешать между
собой несколько газов с различными атомными номерами и затем перевести их
в состояние плазмы, то величина снижения энергии ионизации у всех сортов
атомов будет одинакова. Вызывается это снижение наличием заряженных частиц
в плазме. Причем чем их больше, тем больше оказывается снижение энергии
ионизации. Так как величины снижения энергии других частиц плазмы,
отличных от атомов, таких как ионы, электроны, молекулы, отличаются от
энергии снижения атомов только постоянными множителями, то эти процессы не
зависят напрямую от атомного номера вещества.
Видно, что описанные
процессы универсальны, поэтому было предположено, что именно они
определяют механизм потерь энергии из канала. Представить работу этого
механизма можно следующим образом. Плазменный канал окружает горячий, но
уже нейтральный газ, снижение энергии частиц в нем отсутствует, так как
нет заряженных части. В плазме заряженные частицы присутствуют, а, значит,
энергия всех частиц в плазме понижена. Но энергия ионизации и кулоновская
энергия представляют собой потенциальную форму энергии, поэтому частицам
из окружающего плазму нейтрального газа энергетически выгодно попасть в
плазму и уменьшить свою потенциальную энергию на величину снижения энергии
частиц в плазме.
Отсюда следует, что для поддержания своего
существования плазме разряда необходимо тратить энергию на удаление
поступающих в нее извне частиц. И эту энергию она черпает из источника
тока, питающего разряд. Если от плазмы отключить энергетическую подпитку,
то собственной энергии "на борьбу" с пытающимися "засыпать" ее частицами
хватит не надолго, и она прекратит свое существование, превратившись в
обычный газ.
Существование энергетического барьера, равного по
величине энергии снижения частиц в плазме, между плазменным объемом и
окружающей его областью нейтрального газа позволяет с хорошей точностью
определить мощность, затрачиваемую плазмой "на борьбу" за свое существование.
Действительно, через этот барьер проходят все поступающие в нее частицы,
которые "она заворачивает" обратно, поэтому, если перемножить число
частиц, удаляемых из плазмы через ее границу в единицу времени, на
величину энергии снижения частиц в плазме за счет ее поляризации, то
получится величина мощности неизлучательных потерь энергии из канала,
затрачиваемой плазмой. Очевидно, что эта мощность близка к тепловой
мощности, затрачиваемой на нагрев области газа, окружающего плазму, если
поглощение плазменного излучения мало во внешней области.
В реальных
условиях между центральными горячими областями плазмы и оболочкой из
нейтрального газа находится переходная зона. Такую систему сложно
анализировать, для этого нужно знать радиальные распределения параметров
плазмы канала (см. "Энергобаланс
аргоновой дуги"), поэтому заменим реальный плазменный канал разряда
максимально упрощенной моделью.
Считаем, что плазменный канал разряда
однороден и что он окружен внешней непроводящей зоной нейтрального газа.
Если разряд происходит в трубке, то этой зоной является тонкий
пристеночный слой газа. Отмечу, что в сильноточных ограниченных разрядах
распределение параметров плазмы близко к однородному. Полагаем, что каждая
частица, уходящая из плазмы во внешнюю зону, компенсируется встречной
частицей, то есть происходит как бы отражение от границы
зон. Допускаем, что на удаление каждого вида частицы из плазмы во внешнюю
зону затрачивается энергия, равная величине снижения энергии частиц этого
вида в плазме. Таким образом, можно сказать, что реальный плазменный канал
заменяется при упрощенном анализе цилиндрическими вложенными друг в друга
потенциальными ямами с плоским дном и вертикальными стенками, глубины
которых в энергетических единицах пропорциональны величинам снижения
энергии (потенциальной) частиц в плазме. В этой ситуации очевидно, что
энергия, затрачиваемая на обеспечение стабильности плазменного канала по
каждому виду частиц, равна произведению величины снижения энергии данного
вида частиц помноженному на частоту их соударений со стенками
потенциальной ямы. Хочу еще раз подчеркнуть, что величина снижения энергии
частиц в плазме связана известными соотношениями с температурой
и концентрацией заряженных частиц в плазме [1]. Поэтому она представляет
удобный инструмент, позволяющий понять картину процессов, происходящих в
разряде.
На основе этой модели получено, в частности, аналитическое
выражение для зависимости давления в канале от тока, начального давления
газа в трубке, радиуса трубки и рода наполняющего трубку газа. Вывод его
дан на странице сайта "История исследования
сильноточного..." для случая, когда степень ионизации плазмы не
превышает единицы. Здесь приводится более общее выражение [3], пригодное
для многократно ионизованной плазмы, в виде:
Его отличие от случая, когда степень ионизации плазмы не превышает 1, заключается в появлении множителя zγ-1, входящего в формулу Спитцера для электропроводности полностью ионизованной плазмы. Приведенное выражение проверено в широком диапазоне режимов разряда. Условие его применимости: плазма канала полностью или почти полностью заполняет сечение разрядной трубки.
4. 1. 1. Расчет среднегеометрического модельного значения величины Пp.
Представим выражение (9) для Пp в виде, удобном
для практического применения, упростив его путем подстановки в него
усредненных значений величин: среднего заряда иона в плазме z; величины γ
- функции слабо зависящей от z; кулоновского логарифма lnΛ; степени
ионизации плазмы η; величины δ=W/Q, которая показывает, во сколько раз
излучательные потери энергии из канала разряда превышают неизлучательные
потери, обуславливаемые плазменными поляризационными эффектами; величины
τ, характеризующей, какую долю от поступательной энергии составляет
величина снижения потенциальной энергии частиц в плазме за счет
поляризационных эффектов.
Выражение (9) представляет собой произведение
множителей, точные значения которых для каждого конкретного режима разряда
определить затруднительно. В этой ситуации удобно для характеристики таких
величин использовать среднегеометрические значения из минимальной и
максимальной их величины в предполагаемой области их существования.
Прежде чем проводить указанную процедуру, вспомним
свойства среднегеометрических величин. Если некоторая величина ω может
изменяться в определенных пределах, задаваемых ее минимальным
ω1 и максимальным ω2 значениями, то такую величину
бывает удобно характеризовать среднегеометрическим значением ‹ω›
=(ω1ω2)1/2 величин ω1 и
ω2, а также коэффициентом t(ω)=ω2‹ω›-1
=‹ω›ω1-1, который показывает, какова максимально
возможная кратность отклонения фактического значения ω от ‹ω›.
Из
приведенного определения среднегеометрического значения следует, что,
во-первых, среднегеометрическое произведение нескольких величин равно
произведению среднегеометрических значений каждой величины. Во-вторых,
коэффициент t, характеризующий произведение среднегеометрических значений,
равен произведению аналогичных множителей для каждого
среднегеометрического значения.
Теперь можно приступить к приведению
выражения (9) к рабочему виду. Для простоты ограничимся случаем плазмы со
степенью ионизации не выше единицы. При этом z=1, γ=0,582.
В качестве
первого шага оценим вероятную область изменения величины (1+δ),
входящей в Пp. Пусть в рассматриваемой области режимов доля
излучения может варьироваться в пределах от 20 до 80% от полной мощности,
подводимой к разряду. Это означает, что величина (1+δ) заключена в
пределах 1,25÷5. Величина (1+δ)-1/3 варьируется при этом в пределах 0, 58÷0, 93. Среднегеометрическое значение её равно ‹(1+δ)-1/3›=0, 737, а t(δ)=1, 27.
Величина τ легко рассчитывается для любого диапазона
температур и давлений плазмы. Например, для аргоновой плазмы атмосферного давления величина τ находится в пределах
3·10-3÷1·10-1. Допустим, что этот интервал нам
подходит. Тогда среднегеометрическое значение ‹χ-1/3›=3, 84, а коэффициент
t(τ)=1, 79.
Для широкого диапазона режимов величина
кулоновского логарифма lnΛ находится в пределах 3÷7. Для этого диапазона
‹lnΛ›1/3=1, 66, и t(Λ)=1, 15.
Величина
(1+η)η-1/3≈2 для значений 0,1<η<1.
С учетом
сказанного величину ‹Пp› запишем в виде:
Эта формула позволяет оценивать среднегеометрические значения величины Пp в различных газах. Сопоставление выражения (10) с экспериментальными данными проведено ниже.
4. 1. 2. Экспериментальные значения Пp в различных газах.
В следующих трех таблицах, взятых из [3], приведены
экспериментальные значения величин Пp, которые рассчитаны для
каждого приведенного в таблицах опыта. Обработка велась по следующей
схеме: сначала по известным значениям p, I, po, R
рассчитывалась величина x, входящая в выражение (8), а затем и сама
величина Пp=p/x.
Кратко прокомментирую эти таблицы.
В
первой из представленных таблиц приведены, в основном, опыты, в которых
авторами [2] (ссылка в таблице) с помощью интерферометра измерена концентрация ионов ni и нейтральных атомов na
в импульсных лампах. По этим концентрациям рассчитана температура плазмы Т
с помощью формулы Саха в предположении равновесности плазмы. При достигнутых температурах концентрация электронов
ne=ni. На основании
этих данных при составлении этой таблицы были дополнительно рассчитаны
следующие параметры: давление плазмы p, величина начального давления в
лампах рo, которая была бы в них при нормальных условиях при
работе в режиме без вытеснения газа. Очевидно, что при отсутствии
вытеснения концентрация атомов в лампах при нормальных условиях равна
na+ ne в предположении, что при достигнутых
параметрах плазма однородна по сечению ламп.
Затем на основе комплекта
полученных значений определена величина Пp.
|
Таблица 3. | |||||||||
| № п/п |
Газ | I, кА | ne·10-17, см-3 |
na·10-18, см-3 |
T·10-3, K |
pо, кПа | p·10-5, Па | Пp·102 | Рабо- та |
| 1 | Ar | 0, 38 | 4, 1 | 5, 9 | 12, 8 | 25, 5 | 12, 1 | 9, 31 | [2] |
| 2 | " | 0, 96 | 9, 0 | 4, 5 | 14, 4 | 21, 9 | 12, 8 | 5, 88 | ["] |
| 3 | " | 1, 84 | 25 | 3, 5 | 17, 4 | 24, 3 | 20, 8 | 5, 78 | ["] |
| 4 | Kr | 0, 42 | 4, 9 | 6, 0 | 11, 9 | 26, 1 | 11, 7 | 8, 29 | ["] |
| 5 | " | 0, 77 | 8, 3 | 5, 7 | 12, 9 | 26, 4 | 13, 4 | 6, 29 | ["] |
| 6 | " | 1, 96 | 19, 7 | 4, 4 | 14, 9 | 25, 7 | 17, 5 | 4, 49 | ["] |
| 7 | Xe | 0, 27 | 2, 5 | 1, 5 | 10, 6 | 7, 07 | 3, 0 | 6, 82 | ["] |
| 8 | " | 0, 59 | 5, 4 | 0, 94 | 12, 2 | 6, 0 | 3, 5 | 5, 27 | ["] |
| 9 | " | 1, 08 | 8, 5 | 0, 62 | 13, 7 | 5, 93 | 4, 5 | 4, 56 | ["] |
| 10 | " | 0, 27 | 3, 3 | 7, 2 | 9, 9 | 30, 4 | 11, 0 | 9, 46 | ["] |
| 11 | " | 0, 92 | 9, 3 | 5, 1 | 11, 6 | 24, 4 | 11, 0 | 4, 83 | ["] |
| 12 | Ar | 3, 5 | 4, 5 | 26 | 1, 33 | 1, 40 | 5, 02 | [1] | |
| 13 | " | 3, 54 | 0, 66 | 30 | 0, 133 | 0, 45 | 7, 43 | ["] | |
| 14 | " | 10,0 | 1, 0 | 45 | 0, 133 | 0, 85 | 7, 02 | ["] | |
| [2] - Бакеев А. А., Ровинский Р. Е.– ТВТ. 1970. Т. 8. № 6. С. 1121; Ровинский Р. Е. – ТВТ. 1971. Т. 10. № 1. С. 1; [1] - Пышнов А. В. – ТВТ. 1978. Т. 16. № 5. С. 914. | |||||||||
Во второй таблице приведены результаты измерения давления в трубках различного диаметра, наполненных гелием. Измерения давления выполнены в квазистационарной стадии разрядов. По измеренным значениям давления выполнен расчет значений Пp, реализуемых в разрядах при разных начальных условиях.
|
Таблица 4. | ||||||
| № п/п |
pо, кПа | R·10-3, м | I, кА | p·10-5, Па | Пp·102 | Рабо- та |
| 1 | 0, 4 | 5, 2 | 1, 6 | 0, 5 | 3, 5 | [1] |
| 2 | 0, 4 | 5, 2 | 8, 0 | 2, 9 | 6, 94 | ["] |
| 3 | 1, 33 | 5, 2 | 1, 0 | 1, 1 | 4, 72 | ["] |
| 4 | 1, 33 | 5, 2 | 7, 8 | 5, 34 | 5, 84 | ["] |
| 5 | 10, 13 | 5, 2 | 7, 1 | 18, 0 | 5, 41 | ["] |
| 6 | 0, 133 | 10 | 5, 0 | 0, 30 | 3, 93 | ["] |
| 7 | 0, 133 | 10 | 15, 0 | 1, 02 | 6, 43 | ["] |
| 8 | 1, 33 | 10 | 3, 5 | 1, 10 | 3, 94 | ["] |
| 9 | 1, 33 | 10 | 15, 0 | 3, 20 | 4, 35 | ["] |
| 10 | 20, 3 | 10 | 3, 6 | 15, 0 | 8, 58 | ["] |
| 11 | 20, 3 | 10 | 10, 0 | 29, 0 | 8, 39 | ["] |
| 12 | 81, 0 | 10 | 3, 6 | 20, 1 | 4, 57 | ["] |
| 13 | 81,0 | 10 | 10, 0 | 41, 0 | 4, 72 | ["] |
| 14 | 0, 29 | 20 | 11, 9 | 0, 71 | 6, 22 | ["] |
| 15 | 5, 07 | 20 | 11, 6 | 3, 48 | 4, 60 | ["] |
| 16 | 20, 3 | 20 | 11, 0 | 9, 4 | 5, 10 | ["] |
| 17 | 1, 33 | 26 | 18, 0 | 1, 4 | 4, 38 | ["] |
| 18 | 20, 3 | 26 | 16, 0 | 7, 5 | 4, 12 | ["] |
| 19 | 8106 | 8 | 750 | 28500 | 6, 12 | [18] |
| 20 | 25300 | 8 | 600 | 44800 | 5, 84 | ["] |
| [1] - Пышнов А. В. – ТВТ. 1978. Т. 16. № 5. С. 914; [18]- Березкин А. Н. – Ш Всес. конф. по физике низкотемпературной плазмы. М . : 1971. | ||||||
Наконец, в последней таблице собраны режимы разрядов в различных веществах и, в частности, в тех, которые не изучались на описанной установке.
|
Таблица 5. | |||||||
| № п/п |
Вещество | pо, кПа | R·103, м | I, кА | p·10-5, Па | Пp·102 | Работа |
| 1 | Cs | 264 | 0, 35 | 0, 124 | 130 | 3, 31 | [19] |
| 2 | " | 223 | 0, 35 | 0, 228 | 130 | 3, 31 | ["] |
| 3 | " | 1208 | 0, 35 | 0, 0976 | 350 | 5, 09 | ["] |
| 4 | " | 867 | 0, 35 | 0, 160 | 350 | 4, 57 | ["] |
| 5 | H2 | 0, 133 | 10 | 3, 54 | 0, 30 | 4, 95 | [1] |
| 6 | " | 0, 133 | 10 | 15, 0 | 1, 35 | 8, 51 | ["] |
| 7 | " | 1, 33 | 10 | 3, 5 | 0, 75 | 2, 69 | ["] |
| 8 | " | 1, 33 | 10 | 15, 0 | 3, 52 | 4, 78 | ["] |
| 9 | " | 20, 3 | 10 | 10, 0 | 18 | 5, 2 | ["] |
| 10 | " | 40, 5 | 10 | 10, 0 | 28 | 5, 1 | ["] |
| 11 | N 2 | 0, 133 | 10 | 5, 0 | 0, 45 | 5, 9 | ["] |
| 12 | " | 0, 133 | 10 | 15, 0 | 1, 70 | 10, 7 | ["] |
| 13 | " | 1, 33 | 10 | 5, 0 | 1, 40 | 3, 95 | ["] |
| 14 | " | 1, 33 | 10 | 15, 0 | 3, 50 | 4, 75 | ["] |
| 15 | " | 20, 3 | 10 | 10, 0 | 16, 2 | 4, 68 | ["] |
| 16 | CO2 | 0, 4 | 5, 2 | 5, 35 | 1, 9 | 5, 95 | ["] |
| 17 | " | 7, 73 | 5, 2 | 3, 4 | 10, 2 | 6, 0 | ["] |
| 18 | " | 10, 13 | 5, 2 | 3, 4 | 14 | 6, 88 | ["] |
| 19 | " | 1, 33 | 20 | 11, 6 | 2, 04 | 6, 58 | ["] |
| 20 | " | 5, 07 | 20 | 11, 6 | 4, 8 | 6, 34 | ["] |
| 21 | " | 1, 33 | 5, 2 | 3, 4 | 4, 0 | 7, 6 | ["] |
| 22 | H2O | 432 | 0, 53 | 50 | 3700 | 2, 53 | [20] |
| 23 | " | 57000 | 0, 50 | 125 | 120000 | 1, 62 | ["] |
| 24 | " | 1330 | 2 | 85 | 10000 | 8, 55 | [21] |
| [19] - Барольский С. Г., Ермохин Н. В., Кулик П. П., Мельник В. М. – ЖЭТФ. 1972. Т. 62. № 1 С. 176; [1] - Пышнов А.В. – ТВТ. 1978. Т. 16. № 5. С. 914; [20] - J.W.Robinson. – J.Appl. Phys. 1967. V. 38. № 1. P. 210; [21] - E. Martin. – J. Appl. Phys. 1960. V. 31. № 2. P. 355. | |||||||
4. 1. 3. Основной вывод из сравнения данных экспериментов и модельной зависимости (8).
В таблице 6 приведены рассчитанные с помощью формулы (10) модельные значения среднегеометрических значений величин Пp для различных газов. Напомню, что эта формула записана для случая, когда средний заряд иона в плазме не сильно отличается от 1. Этому условию при всех значениях тока удовлетворяет только плазма водорода. В остальных газах этот случай реализуется при разрядах, формируемых при относительно высоких начальных давлениях газа и относительно низких амплитудах тока. При значительных амплитудах тока средний заряд иона может достигать значений 3-4. Если в одноатомном плазмообразующем газе газе средний заряд иона равняется 2, то согласно формуле (9) величина Пp будет равна 4,06.
|
Таблица 6. | |||||
| № п/п |
Газ | q | Модельные значения Пp·102 |
Экспериментальные значения | |
| Пp·102 | t(Пp) | ||||
| 1 | H2 | 2 | 4, 3 | 4, 8 | 1, 8 |
| 2 | He | 1 | 2, 7 | 3, 4 | 1, 6 |
| 3 | Ar | 1 | 2, 7 | 6, 8 | 1, 4 |
| 4 | Kr | 1 | 2, 7 | 6, 1 | 1, 4 |
| 5 | Xe | 1 | 2, 7 | 6, 6 | 1, 5 |
| 6 | Cs | 1 | 2, 7 | 4, 1 | 1, 3 |
| 7 | N2 | 2 | 4, 3 | 6, 5 | 1, 7 |
| 8 | CO2 | 3 | (5, 7) | 6, 4 | 1, 1 |
| 9 | H2O | 3 | (5, 7) | 3, 7 | 2, 3 |
| Расчетное модельное значение t(Пp) для всех газов одинаково и равно 2,6. | |||||
Сравнение экспериментальных значений Пp, приведенных в таблицах (3-5), и модельных значений из таблицы (6) показывает их удовлетворительное согласие. Это может свидетельствовать только о том, что, действительно, плазменные поляризационные эффекты играют важную роль в электрическом разряде. Учет этих эффектов приводит к зависимостям, количественно описывающим состояние плазмы канала разряда.
В таблице 6, представляющей расширенный вариант таблицы
из [3] под тем же номером, приведены экспериментальные
среднегеометрические значения величин Пp, рассчитанные на
основе массивов данных в таблицах (3-5), относящихся к различным газам.
Расчет велся следующим образом: из массива данных, относящихся к
выбранному газу, бралось максимальное и минимальное значение величины
Пp и затем по ним рассчитывалось экспериментальное
среднегеометрическое значение. Полученные значения приведены в
предпоследнем столбце таблицы. Видно, что согласие с модельными значениями
удовлетворительное.
В итоге можно
сказать, что поляризационные плазменные процессы составляют тот фундамент,
на котором следует развивать практичную теорию электрического
разряда.
4. 2. Каналовая модель дуги, учитывающая поляризацию плазмы.
Предложена модернизация классической каналовой модели дуги. Учет поляризационных плазменных процессов в этой модели позволил получить аналитическое выражение [3] для температуры в стабилизированных стенками дугах через их внешние параметры, согласующееся с экспериментами, что служит еще одним доказательством фундаментальной роли данных процессов в разряде. Подробно полученные результаты изложены на странице "Каналовая модель электрической дуги".
4. 3. Время распада плазменных образований, содержащих щелочноземельные элементы.
Учет плазменных эффектов позволяет записать выражение для
оценки времени жизни плазменного образования, причем особенно просто это
выражение выглядит для следующего специфического случая.
Принято
думать, что для создания плазмы нужны высокие температуры, но это не
совсем так. Плазму даже сильноионизованную можно создать и при
температурах, которые превышают комнатную примерно в два раза, если
считать по шкале Кельвина. Действительно, у щелочноземельных элементов
(цезия, рубидия, калия) величина энергии ионизации мала, в пределах
3,9-4,4 эв. Причем энергия ионизации димерных молекул этих элементов будет
еще ниже, в пределах 3, 65-3, 90 эв [4]. Например, у молекулы Cs2
энергия ионизации равна 3, 65 эв, а у молекулы K2 - 3, 90 эв.
Температура плавления щелочноземельных элементов находится в пределах
29-80°C, а кипения 690-770°C при атмосферном давлении. Упругость паров
цезия, рубидия, калия уже при температурах, не превышающих 340°C, становится
более 1 мм рт. ст., что соответствует примесной концентрации этих
элементов в газовой смеси > 1·1016, см-3. Если
пары этих элементов смешать с газом, состоящим из элементов с высокой
степенью ионизации, и нагреть эту смесь до температур, величина которых
будет выше примерно 600°С, то получим плазму, так как атомы
щелочноземельных элементов будут полностью ионизованы при этой
температуре. А известно, что газ, в котором есть заряженные частицы в
достаточном количестве, и есть плазма. При этом частицы газа с высоким
потенциалом ионизации в этой смеси останутся практически неионизованными.
Регулируя количество примеси щелочноземельных элементов в смеси, можно при
одной и той же температуре получить низкотемпературную плазму с различной
степенью ионизации. Причем, что крайне важно, снижение энергии всех частиц
в такой плазме, как ионизованных так и нет, будет одинаковым. Таким
образом, концентрация щелочноземельных элементов регулирует величину
снижения энергии ионизации всех атомов смеси, причем величина этого
снижения в достаточно широком температурном интервале не будет зависеть от
температуры, так как все атомы примеси полностью ионизованы, начиная с
некоторого значения температуры.
Как показано на странице "Гипотеза о механизме
шаровой молнии" скорость остывания нагретого модельного шара газа
зависит от величины снижения энергии ионизации. Это означает, если в шаре
присутствуют щелочноземельные элементы, определяющие величину снижения
энергии ионизации, то чем меньше их концентрация в шаре, тем медленнее он
остывает. Прикидка показывает, что если в шаре диаметром 20 см, нагретом
до 1000K, концентрация щелочноземельного элемента составляет величину
108, см-3, то время остывания такого шара будет 2, 4
сек. Если концентрация будет на два порядка ниже, то время остывания
составит уже 24 сек. Модельное время остывания пропорционально диаметру
шара. Это означает, что для шара диаметром в 1 метр модельное значение
продолжительности остывания может быть от 12 до 120 секунд для указанной
выше концентрации примесных атомов. Однако при величине примесной
концентрации 1010, см-3, модельное время остывания
для метрового шара не превысит 12 сек.. Таким образом, с этой позиции
шаровая молния может представлять нагретый газовый шар, содержащий очень
малое количество элементов с низким значением энергии ионизации. Такая
точка зрения позволяет объяснить многие ее наблюдаемые свойства. Например,
почему вещество шаровой молнии можно разделить на несколько частей, а
затем соединить их обратно. Или, почему она с легкостью может проникать
сквозь узкие отверстия, щели и т. д.. Это просто нагретый газ, поэтому для
проникновения молнии через отверстие теплопроводность материала стенок
отверстия должна быть мала, чтобы первые порции молнии смогли бы нагреть
их до температуры, при которой вещество молнии остается в состоянии
плазмы, а не превращается в результате охлаждения в обычный газ.
С
рассмотренной позиции также легко ответить на вопрос, что, если все дело в
присутствии щелочноземельных элементов, то почему большинству людей не
удается увидеть ее ни разу в жизни. Я, например, за свои 68 лет ни разу не
увидел ее ни в грозу, ни в ясную погоду, в комнату ко мне она также не
залетала. А дело в том, что щелочноземельные элементы широко
распространены, а для существования шаровой молнии нужна чрезвычайно
низкая их концентрация в атмосфере, которая, видимо, реализуется
достаточно редко. Ведь, представьте себе, что нужна концентрация порядка
108 в кубическом сантиметре, а концентрация частиц в атмосфере
равна 1019, то есть разница 11 порядков! Таким образом,
появление шаровой молнии означает, что концентрация щелочноземельных
элементов в атмосфере стала чрезвычайно низкой.
В принципе, мы, видимо,
часто сталкиваемся с шаровыми молниями, только короткоживущими, то есть
такими, у которых высока концентрация щелочноземельных элементов.
Например, даже при концентрации их 1012, см -3
время жизни молнии диаметром 20 см будет около 0, 024 сек, поэтому такую
шаровую молнию заметить невозможно.
На странице "Гипотеза о механизме
шаровой молнии" описаны опыты, суть которых заключалась в инициировании
разрядов сильноточными импульсами малой длительности не более 50
наносекунд или, другими словами, не более 5 × 10-8
секунды. Амплитуда тока в импульсах доходила до 16 кА. В ксеноне такими
импульсами стабильно создавались разряды, плазма которых заполняла весь
объем трубки, а время свечения ее было чуть более 1 сек, причем
характерный размер объема плазмы составлял 10 см. Ксенон был изотопной
чистоты, то есть, вероятно, достаточно чистый. Нашелся он случайно на
лабораторном складе в запаянных стеклянных шарообразных баллонах диаметром
сантиметров 20, наполненных до давления 600 мм рт. ст.. Если модельный,
вывод о том, что время жизни плазменного шара пропорционально его радиусу,
верен, то время свечения шара диаметром 20 см в этом ксеноне должно было
бы быть чуть более двух секунд. Случайное это совпадение с модельной
оценкой или нет, не знаю.
Эти опыты проводились примерно в 1976, а
приведенное истолкование этого результата появилось только около 1991
года, причем в публикации его мне тогда в журнале ЖТФ отказали. Тоже
своеобразный парадокс - одни (например, И. П. Стаханов, собиравший
сведения о шаровой молнии с помощью анкеты, опубликованной в журнале
"Наука и жизнь") ищут очевидцев, которые наблюдали долгосветящиеся
объекты, а посылаешь в научный журнал описание опыта, в котором описано
получение такого образования в лаборатории, причем с гипотезой,
предлагающей объяснение наблюдаемого феномена - то получаешь отказ.
Загадочная штука жизнь, загадочнее шаровой молнии.
Из вышесказанного
следует, что скорость остывания нагретого газового шара определяется
концентрацией в нем элементов с низким потенциалом ионизации, причем, чем
меньше эта концентрация, тем медленнее остывает шар. То есть концентрация
полностью ионизованных при относительно низких температурах атомов легко
ионизирующейся примеси является регулятором скорости остывания плазменного
газового шара. Оценки показывают, что время остывания такого шара может
сравняться по продолжительности с наблюдаемым временем существования
шаровой молнии.
В связи с выше сказанным представляет интерес
процитировать выдержку из книги М. Юмана "Молния" [5] из той ее части, где
характеризуются известные теории шаровой молнии. Итак, теория под номером
1: "Шаровая молния представляет собой газ или воздух, обладающий
необычными свойствами. Предполагалось, что шаровая молния - это медленно
горящий газ; излучение за счет медленной рекомбинации неизвестных ионов;
излучение долгоживущих частиц воздуха, находящихся в метастабильных
состояниях, или частиц которым передается энергия метастабильных частиц;
химическая реакция, в которой принимают участие пыль, копоть, и т.
д."
Из приведенной цитаты видно, что на момент появления книги М. Юмана
в 1969 г. объяснить шаровую молнию пытались за счет некоего механизма,
обеспечивающего весьма низкую скорость потерь энергии из газового шара.
Впоследствии эта идея была развита и появилась, в частности, известная
кластерная гипотеза шаровой молнии, предложенная И.П. Стахановым в
середине 70-х годов. Стаханов, как и многие другие физики, исходил из
представления, что шаровая молния состоит из вещества в состоянии плазмы.
То есть вещества, содержащего заряженные частицы, которые по мере его
охлаждения рекомбинируют и плазма превращается в обычный газ. Причем
процесс рекомбинации проходит быстро за времена существенно меньшие 1
секунды. Стаханов предположил, что ионы при низких температурах (200-300°С)
могут окружать себя оболочкой из молекул воды (образуется, так называемый,
кластер), обладающих, как известно, сильным "полярным" эффектом, которая
сильно затруднит процесс их рекомбинации с электронами. Поэтому время
существования такой "насыщенной водой" плазмы, может сравняться с временем
существования шаровой молнии.
Я не знаю, смогли ли получить в
лаборатории шаровую молнию на основе кластерной гипотезы. Но, могу
отметить, что осмысление роли поляризационных плазменных процессов в
разрядах позволило предложить новую отличную от всех ранее известных
гипотезу о её природе, изложенную выше. Представляется, что эта гипотеза,
наравне с кластерной, может объяснить большинство известных свойств
шаровой молнии, но не нуждается в кластерах, которые, лично мне,
представляются вещью в себе. Кластеры не нужны потому, что
щелочноземельные элементы уже при температурах порядка 500-600°C и выше
полностью ионизованы, поэтому рекомбинации здесь нет, а время остывания
плазменного шара обратно пропорционально корню квадратному из их концентрации. Согласно
оценкам, для получения долгоживущего плазменного шара требуется лишь
ничтожное присутствие щелочноземельных элементов в веществе шара. Такие
ситуации в природных условиях, вероятно, крайне редко, но возникают. Из-за
этого шаровая молния и представляется загадочным явлением. Просто в мире,
где все перемешано, не часто реализуются состояния среды, в которой бы
присутствовали в ничтожно малых количествах широко распространенные
щелочноземельные элементы.
Проводя аналогию, можно сказать, что данная
ситуация напоминает ситуацию с инверсной заселенностью атомных уровней,
которая в обычных условиях существовать просто не может. Но, когда
научились создавать неравновесную плазму с такой заселенностью, то
появились лазеры, которых до этого и в помине не было, и которые воочию
показали, что такая заселенность уровней возможна.
Заключение
- Возникшие сомнения в возможности использования ЛТР методов диагностики плазмы в условиях ограниченного сильноточного многокилоамперного разряда, впервые подробно исследуемого на режимах ранее недоступных, заставили на количественном уровне отработать методику измерения давления в сильноточном ограниченном стенками разряде.
- Анализ обширных результатов измерений давления, добытых с помощью собранной экспериментальной установки и созданной методики измерения давления, привел, в свою очередь, к пониманию основополагающей роли поляризационных процессов в плазме для физики разряда, заставляющей заняться пересмотром существующих представлений о разряде.
- Учет поляризационных плазменных процессов в энергобалансе канала разряда привел к модельным зависимостям, описывающим связь между параметрами реального разряда, которые согласуются с экспериментами, подтверждая тем самым роль упомянутых процессов в разряде.
- На основе учета поляризационных процессов предложена модель шаровой молнии, которая, как представляется, может пролить свет на ее природу, позволяет объяснить все ее существенные свойства, намечает конструктивные пути ее лабораторного воспроизведения и исследования.
- Griem H. R. Phys. Rev. - 1962. V. 128. No.3. P. 997-1006.
- Грим. Г. Спектроскопия плазмы. Пер. с англ./ Под ред. Г. В. Шолина и Г. Е. Смолкина. - М.: Атомиздат, 1969.
- Пышнов А. В. К вопросу построения модели канала квазистационарной сильноточной ограниченной стенками дуги. - М.: Деп. ВИНИТИ № 6889-В89 1989. 35 с.
- Старовойтов Е. М. Потенциалы ионизации, поляризуемости и параметры межмолекулярного взаимодействия индивидуальных веществ в газовой фазе.
- Юман. М. Молния. Пер. с англ. /Под ред. Красногорской Н. В. – М.: Мир, 1972.
- О. А. Малкин. Импульсный ток и релаксация в газе. – М.: Атомиздат, 1974.
♦ ♦ ♦
P. S. В основу этой страницы
положен наиболее полный первоначальный вариант кандидатской диссертации,
защита которой была назначена на 09. 06. 1975 г., но была отложена из-за
отрицательного отзыва оппонирующей организации. В организации не поверили
в вывод о нарушении чЛТР в плазме исследуемых разрядов, несмотря на то,
что ранее этот вопрос никто экспериментально не исследовал. Ведь, в данной
работе впервые была получена газоразрядная квазистационарная плазма,
пригодная для точных спектроскопических исследований, с параметрами,
которые ранее были недоступны. Если я не ошибаюсь, то за прошедшие три
десятилетия эти опыты никто не повторил.
Диссертация была защищена 20.
12. 1976 г.. Положительный отзыв был получен после изъятия из
первоначального варианта результатов, указывающих на отклонение плазмы
азота и аргона от чЛТР, объем которых составил 34, 4% от первоначального
объема диссертации.
Интересно заметить, что у другой оппонирующей
организации названные результаты, но, в менее полном объеме (только те,
которые получены во время совместной работе), не вызвали сомнения,
поэтому организация дала положительный отзыв на защиту докторской
диссертации. Последняя состоялась 16. 04. 1973 г. Упомянутая доля
результатов рассмотрена в книге [6], опубликованной по материалам
докторской диссертации.
Страница размещена на сайте http://polarization.narod.ru/
21 октября 2006 г.